![]()
![]()
![]()
长方体和正方体的体积
教材第29、第30页的内容及练习七第8~10题。
![]()
1. 结合具体情境和实践活动,探索并掌握长方体、正方体的体积的计算方法,能正确计算长方体、正方体的体积。
2. 通过“猜想—验证”的过程,获取数学活动经验。
3. 在观察、操作、探索的过程中,提高动手操作能力,进一步发展空间观念,并解决一些简单的实际问题。
![]()
重点:理解长方体和正方体的体积公式的推导过程,掌握计算方法。
难点:理解长方体和正方体的体积公式的推导过程。
![]()
投影仪,小正方体若干,长方体、正方体教具。
![]()
![]()
![]()
师:我们知道了每个物体都有一定的体积,我们也知道可以利用数单位体积的方法计算物体的体积。
师:要想知道老师手中的这个长方体和正方体的体积,你有什么办法?(先将它切成1立方厘米或1立方分米的小正方体后,再数一数)
说明:用拼或切的方法看它有多少个体积单位。但是在实际生活中,有许多物体是切不开或不能切的,如冰箱、电视机等,怎样计算它们的体积呢?这节课我们就来研究长方体和正方体的体积。(板书)
【设计意图:让学生联系实际生活,从实际中发现数学问题,启发学生思考,从而激发学生的学习欲望,调动学生学习的积极性,让学生主动学习】
![]()
1.探究长方体的体积公式。
师:怎样知道一个长方体的体积是多少呢?
生:如果我们能把它切成一些小正方体就好了。
师:看一看下面的长方体的体积是多少。为什么?
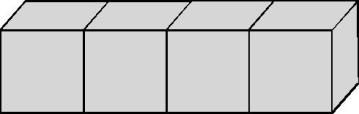
生:体积是4立方厘米。因为它含有4个1立方厘米的体积单位。
师:下面我们运用1立方厘米的体积单位来研究长方体的体积计算方法。再加上这样的两排,这个长方体的体积是多少?你是怎么想的?
生:12立方厘米。
师:怎么得到的?
生:1排是4立方厘米,3排就是4×3=12(立方厘米)。
师:再加上这样的一层,这个长方体的体积是多少?你是怎么计算的?
生:1层是12立方厘米,2层就是12×2=24(立方厘米)。
师:这个长方体的长、宽、高分别是多少?
生:长是4厘米,宽是3厘米,高是2厘米。
板书:体积 长 宽 高
24 4 3 2
师:观察板书上的几个数字之间有什么关系?大胆猜测体积与什么有关?有什么关系?
生1:与长、宽、高有关。因为表面积就与长、宽、高有关。
生2:长方体的体积=长×宽×高……
师:这个猜想正确吗?下面就请同学们通过实验去验证我们的猜想是否正确。
请同学们小组合作,用这些1立方厘米的小正方体木块拼成形状不同的长方体,每拼成一种。就记录下它的长、宽、高和体积各是多少,然后验证刚才的猜想是否正确。全班同学以小组为单位,进行分工,开始操作、计算、记录、思考、讨论,引导学生参与公式的推导,明确小组学习的任务。
师:刚才老师把同学们的实验数据汇总在这张表上了,我们一起来观察。
长 |
宽 |
高 |
小正方体的数量 |
长方体的体积 |
4 |
1 |
1 |
4 |
4 |
3 |
2 |
2 |
12 |
12 |
5 |
2 |
3 |
30 |
30 |
6 |
2 |
1 |
12 |
12 |
师:观察上面表格里的结果,你们发现了什么?
生:长方体所含体积单位的数量就是长方体的体积。
师:每排个数、排数、层数与体积有什么关系?每排个数、排数、层数相当于长方体的什么?
生:因为每一个小正方体的棱长都是1厘米,所以,每排摆几个小正方体,长正好是几厘米;摆几排,宽正好是几厘米;摆几层,高也正好是几厘米。
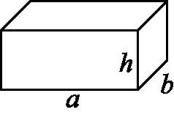
小结:长方体的体积=长×宽×高。 如果用字母V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:V=abh。
2. 迁移得出正方体的体积计算公式。
教师指着长、宽、高都是6厘米的长方体,提问:这个图形有什么特征?正方体的体积的计算方法是什么?
学生讨论后得出:正方体的体积=棱长×棱长×棱长,用字母表示:V=a×a×a=a3
说明理由:正方体是特殊的长方体。
【设计意图:让学生根据长方体和正方体的关系,来推断正方体的体积的计算公式,使学生感觉新知识不难理解,实现平稳过渡,培养学生的推理能力】
3.投影出示例1。
师:这两个图形各是什么图形,应该用哪个公式进行计算?
请同学们自己独立完成。学生计算,教师巡回指导。
学生做完后展示:
V=abh V=a3
=7×3×4 =6×6×6
=84(cm3) =216(dm3)
![]()
这节课我们共同探究了长方体和正方体的体积公式,同学们都积极地动手动脑,总结出了它们的计算公式。
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
V=abh V=a3
![]()
长方体和正方体的体积
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
V=abh V=a3
A类
1. 判断。(对的在括号里画“”,错的画“✕”)
(1)一个正方体的棱长是2米,它的体积是8立方米。 ( )
(2)一个长方体长30厘米、宽2分米、高5厘米,它的体积是30×2×5=500(立方厘米)。 ( )
(3)一个棱长为6分米的正方体,它的表面积和体积相等。 ( )
2. 一个长方体长7厘米、宽4厘米、高3厘米,它的体积是多少?
3. 一块正方体的石料,棱长是6分米,这块石料的体积是多少立方分米?
B类
1. 一块砖的长是24厘米,宽是长的一半,厚是6厘米,它的体积是多少立方厘米?
2. 一个正方体的棱长总和是36厘米,它的体积是多少?

课堂作业新设计
A类:
1. (1) (2)✕ (3)✕
2. 7×4×3=84(立方厘米)
3. 6×6×6=216(立方分米)
B类:
1. 24×12×6=1728(立方厘米)
2. 36÷12=3(厘米) 3×3×3=27(立方厘米)
教材习题
教材第32页练习七
8. 50厘米=0.5米 50×30×0.5=750(立方米) 750立方米=750方
9. 30×30×30=27000(立方厘米)
10. 2×2×0.6=2.4(立方分米) 2.4÷4=0.6(立方分米)