数学试卷（理科）
第Ⅰ卷（共60分）
一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项
是符合题目要求的.
1.已知全集
，集合
，
，则图中阴影部分表示的集合为（
）
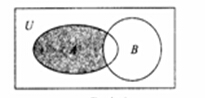
A．
B．
C．
D．
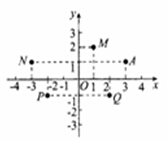
2.已知
为虚数单位，图中复平面内的点
表示复数
，则表示复数
的点是（
）
A．
B．
C．
D．
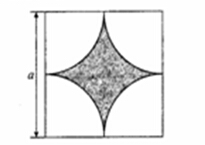
3.如图所示，墙上挂有边长为
的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为
的圆弧，某人向此板投镖.假设每次都能击中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是（
）
A．
B．
C．
D．与
的取值有关
4.某公司为确定明年投入某产品的广告支出，对近5年的广告支出
与销售额
（单位：百万元）进行了初步统计，得到下列表格中的数据：
经测算，年广告支出
与年销售额
满足线性回归方程
，则
的值为（
）
A．45
B．50
C.55 D．60
5.已知焦点在
轴上的双曲线
的中点是原点
，离心率等于
.以双曲线
的一个焦点为圆心，1为半径的圆与双曲线
的渐近线相切，则双曲线
的方程为（
）
A．
B．
C.
D．
6.已知某几何体的三视图如图所示，则该几何体的体积为（ ）
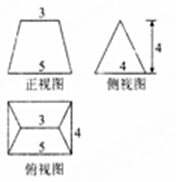
A．
B．35
C.
D．
7.公元263年左右，我国数学家刘徽发现当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了割圆术.利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图，则输出的
为（
）
（参考数据：
,
,
）
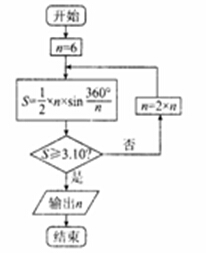
A．12 B．24 C. 36 D．4
8.如图，周长为1的圆的圆心
在
轴上，顶点
，一动点
从
开始逆时针绕圆运动一周，记走过的弧长
，直线
与
轴交于点
，则函数
的图象大致为（
）
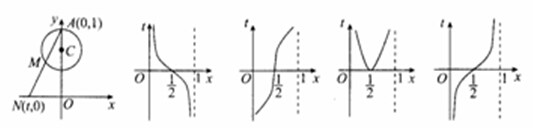
A． B． C. D．[来源:Zxxk.Com]
9.三棱锥
的外接球为
球
，球
的直径是
，且
，
都是边长为1的等边三角形，则三棱锥
的体积是（
）[来源:Z&xx&k.Com]
A．
B．
C.
D．
10.
在
中，角
，
，
的对边分别为
，
，
，且
.若
的面积
，则
的最小值为（
）
A．
B．
C.
D．3
11.已知直线
与函数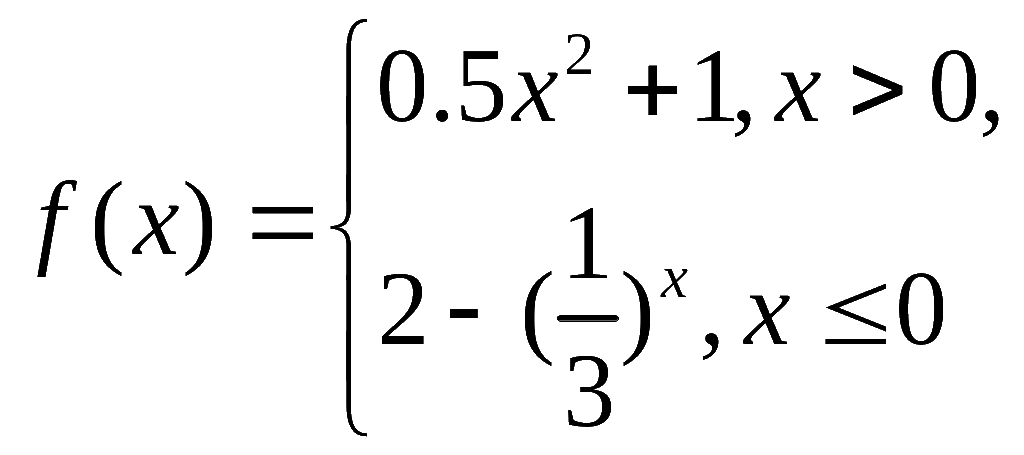
的图象恰好有3个不同的公共点，则实数
的取值范围是（
）
A．
B．
C.
D．
12.已知直线
分别与函数
和
交于
两
点，则
之间的最短距离是（
）
A．
B．
C.
D．
第Ⅱ卷（共90分）
二、填空题（每题5分，满分20分，将答案填在答题纸上）
13.若
的展开式中含有常数项，则
的最小值等于________.[来源:Z*xx*k.Com]
14.已知抛物线方程为
，焦点为
，
是坐标原点，
是抛物线上的一点，
与
轴正方向
的夹角为
，若
的面积为
，则
的值为__________.
15.在送医下乡活动中，某医院安排甲、乙、丙、丁、戊五名医生到三所乡医院工作，每所医院至少安排一名医生，且甲、乙两名医生不安排在同一医院工作，丙、丁两名医生也不安排在同一医院工作，则不同的分配方法总数为__________.
16.若不等式组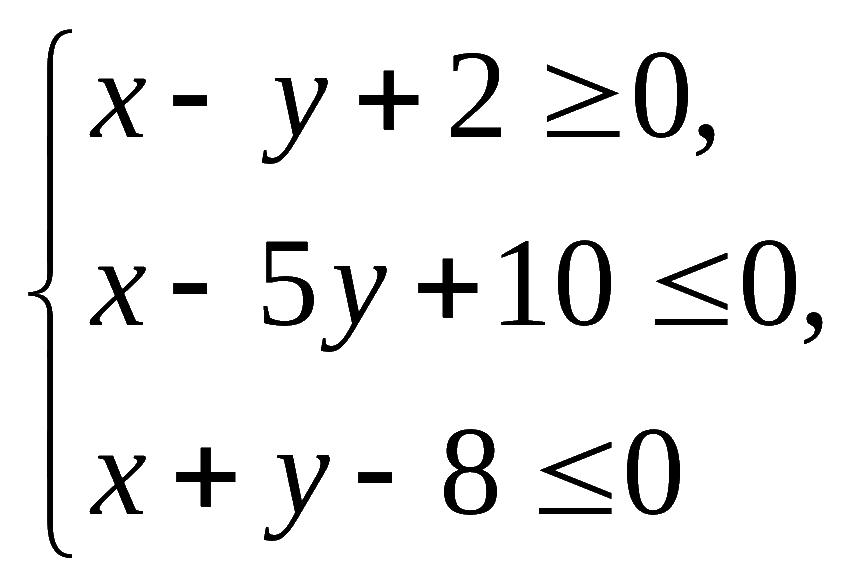
，所表示的平面区域存在点
，使
成立，则实数
的取值范围是___________.
三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）
17.（本小题满分12分）
设数列
的前
项和为
，
,且
为等差数列
的前三项.
（1）求数列
,
的通项公式；
（2）求数列
的前
项和.
18.（本小题满分12分）
某市积极倡导学生参与绿色环保活动，其中代号为“环保卫士-12369”的绿色环保活动小组对2015年1月～2015年12月（一年）内空气质量指数
进行监测，下表是
在这一年随机抽取的100天统计结果：
（1）若该市某企业
每天由空气污染造成的经济损失
（单位：元）与空气质量指数
（记为
）的关系为：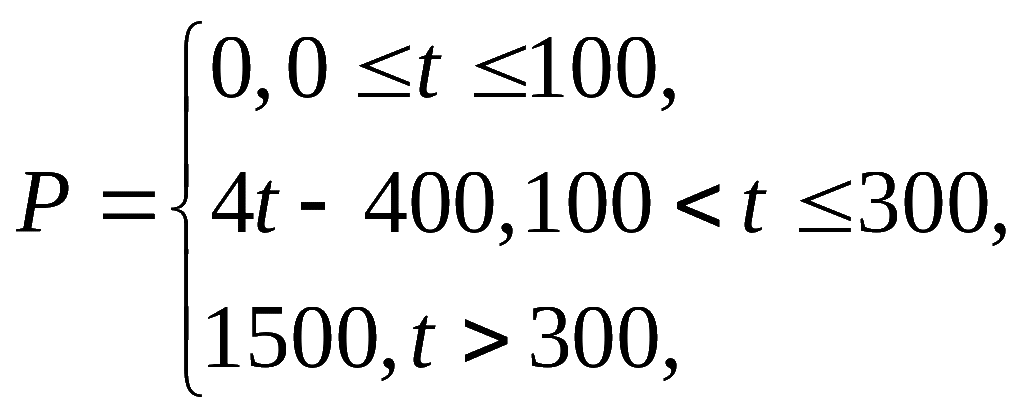
，在这一年内随机抽取一天，估计该天经济损失
元的概率；
（2）若本次抽取的样本数据有30天是在供暖季节，其中有8天为重度污染，完成2×2列联表，并判断是否有95%的把握认为该市本年度空气重度污染与供暖有关？[来源:Zxxk.Com]
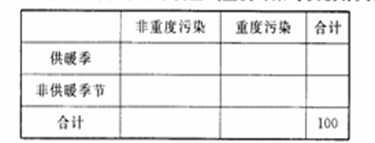
下面临
界值表供参考：
参考公式：
，其中
.
19. （本小题满分12分）
已知在三棱柱
中，侧面
为正方形，延长
到
，使得
，平面
平面
，
，
.
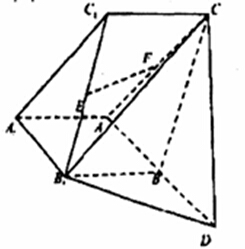
（1）若
分别为
，
的中点，求证：
平面
；
（2）求平面
与平面
所成的锐二面角的余弦值.
20.（本小题满分12分）
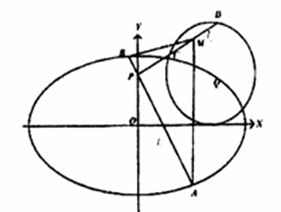
已知椭圆
，圆
的圆心
在椭圆
上，点
到椭圆
的右焦点的距离为
.
[来源:Z|xx|k.Com]
（1）求椭圆
的方程；
（2）过点
作互相垂直的两条直线
，且
交椭圆
于
两点，直线
交圆
于
两点，
且
为
的中点，求
面积的取值范围.
21.（本小题满分12分）
已知函数
，且曲线
与
轴切于原点
.
（1）求实数
的值；
（2）若
恒成立，求
的值.
请考生在22、23中任选一题作答，如果多做，则按所做的第一题记分.
2
2.（本小题满分10分）选修4-1：坐标系与参数方程
已知曲线
的极坐标方程是
，以极点为原点，极轴为
轴的正半轴建立平面直角坐标系，直线
的参数方程为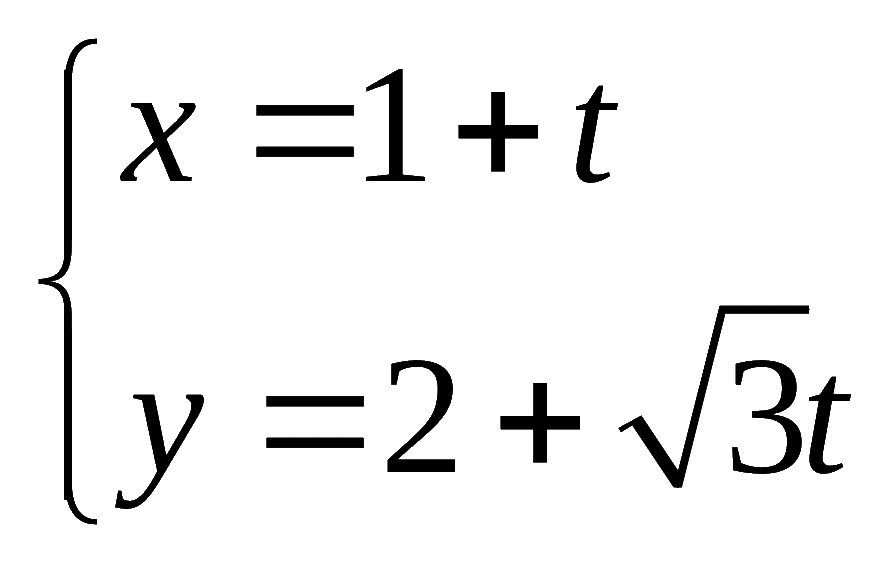
（
为参数）.
（1）写出直线
的普通方程与曲线
的直角坐标方程；
（2）设曲线
经过伸缩变换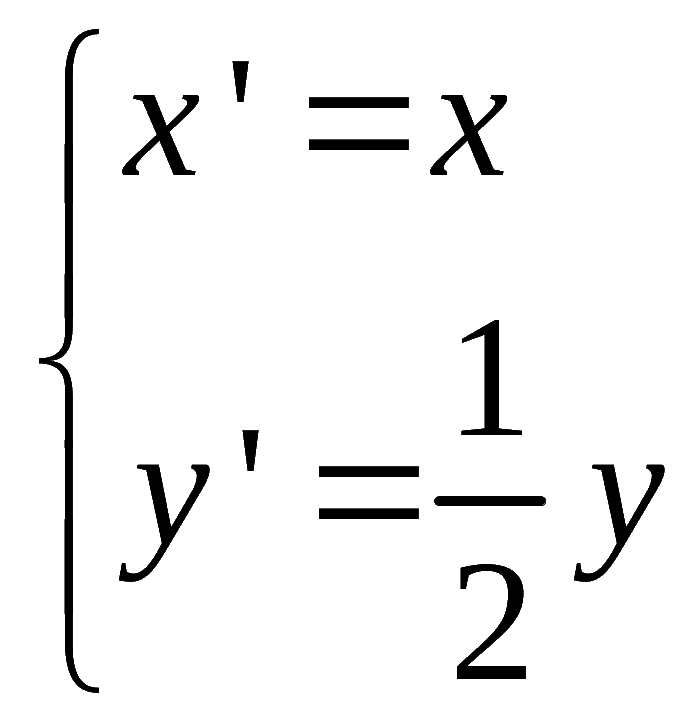
得到曲线
，设
为曲
线
上任一点，求
的最小值，并求相
应点
的坐标.
23.（本小题满分10分）选修4-5：不等式选讲
已知实数
，
，函数
的最大值为3.
（1）求
的值；
（2）设函数
，若对于
均有
，求
的取值范围.
