二次函数
[时间:90分钟 分值:120分]
一、选择题(每小题3分,共30分)
1.下列函数中,当x<0时,y随x的增大而减小的函数是( A )
A.y=-3x B.y=4x
C.y=- D.y=-x2
【解析】 B,C,D中当x<0时,y随x的增大而增大.
2.抛物线y=3(x-1)2+1的顶点坐标是( A )
A.(1,1) B.(-1,1)
C.(-1,-1) D.(1,-1)
【解析】
抛物线y=a(x-h)2+k的![]() 顶点坐标为(h,k).
顶点坐标为(h,k).
3.把二次函数y=-3x2的图象向右平移2个单位,再向下平移1个单位,所得到的图象对应的二次函数解析式是( C )
A.y=-3(x-2)2+1
B.y=-3(x+2)2-1
C.y=-3(x-2)2-1
D.y=-3(x+2![]() )2+1
)2+1
【解析![]() 】
移动规律是:左加右减,上加下减.
】
移动规律是:左加右减,上加下减.
4.对于二次函数y=2(x+1)(x-3),下列说法正确的是( C )
A.图象的开口向下
B.当x>1时,y随x的增大而减小
C.当x<1时,y随x的增大而减小
D.图象的对称轴是直线x=-1
5.图1是反映铅球运动员掷铅球的高度y m与水平距离x m之间的函数关系的图象,其函数解析式为y=-x2+x+,则该运动员此次掷铅球的成绩是( D )
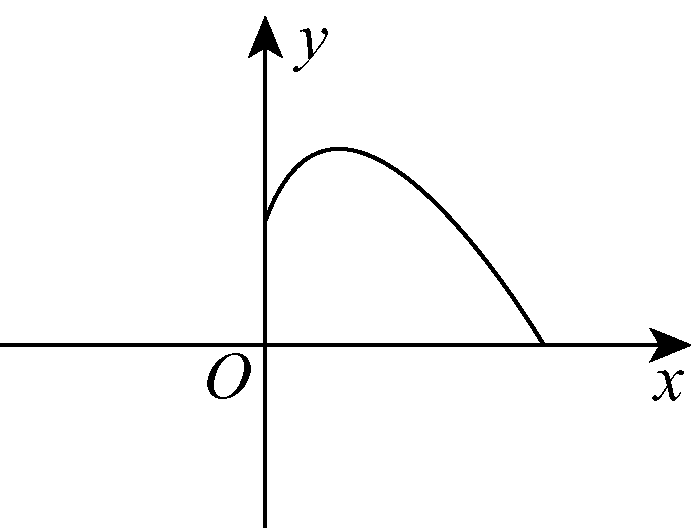
图1
A.6 m B.12 m C.8 m D.10 m
【解析】 令y=0得-x2+x+=0,解得x1=10,x2=-2(舍去).
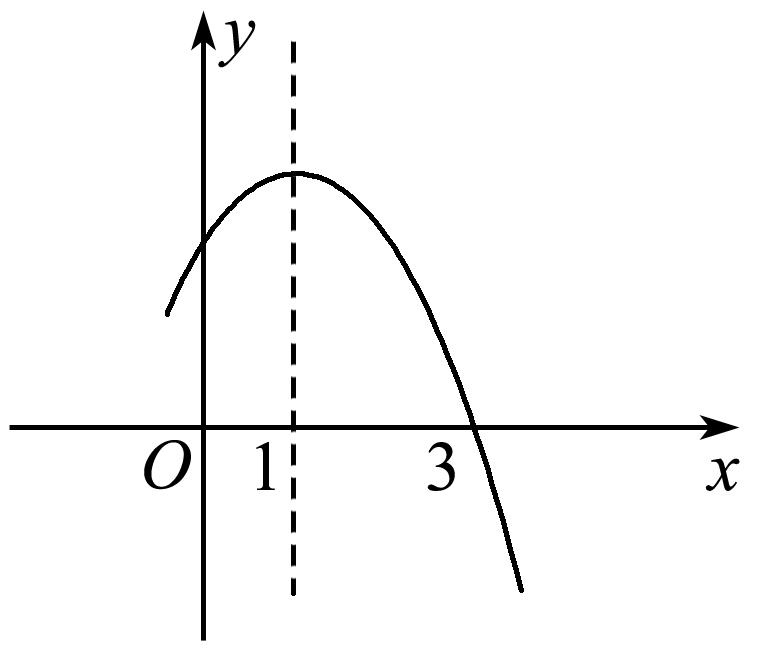
图2
6.二次函数y=-x2+2x+k的部分图象如图2所示,则关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=( B )
A.1 B.-1
C.-2 D.0
7.已知函数y=-x2+x+2,则当y<0时,自变量x的取值范围是( A )
A.x<-1或x>2
B.-1<x<2
C.x<-2或x>1
D.-2<x<1
【解析】 当y=0时,-x2+x+2=0,
(x+1)(-x+2)=0,
x1=-1,x2=2,
由于函数图象开口向下,
可知当y<0时,自![]() 变量x的取值范围是x<-1或x>2.
变量x的取值范围是x<-1或x>2.
8.抛物线图象如图3所示,根据图象,抛物线的解析式可能是( C )
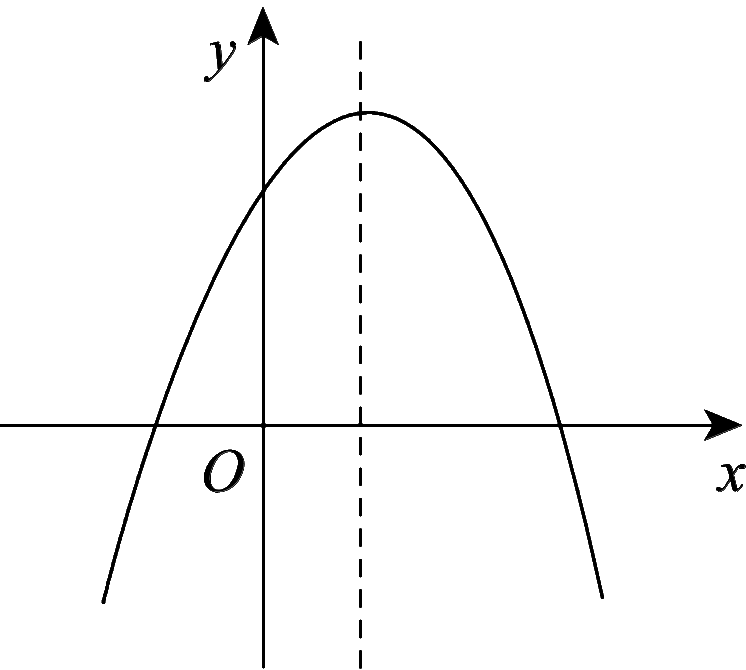
图3
A.y=x2-2x+3
B.y=-x2-2x+3
C.y=-x2+2x+3
D.y=-x2+2x-3
【解析】 抛物线图象开口向下,∴a<0;抛物线图象对称轴在y轴的右侧,∴a,b异号,∴b>0;抛物线图象交y轴于正半轴,∴c>0,故选C.
9.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( B )
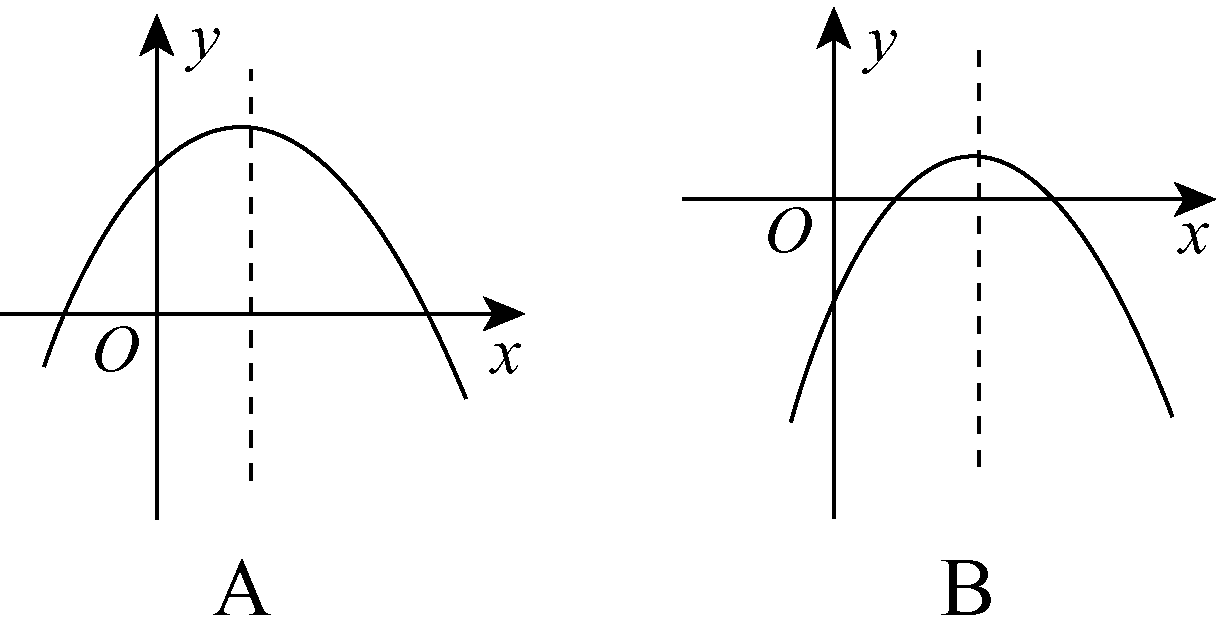
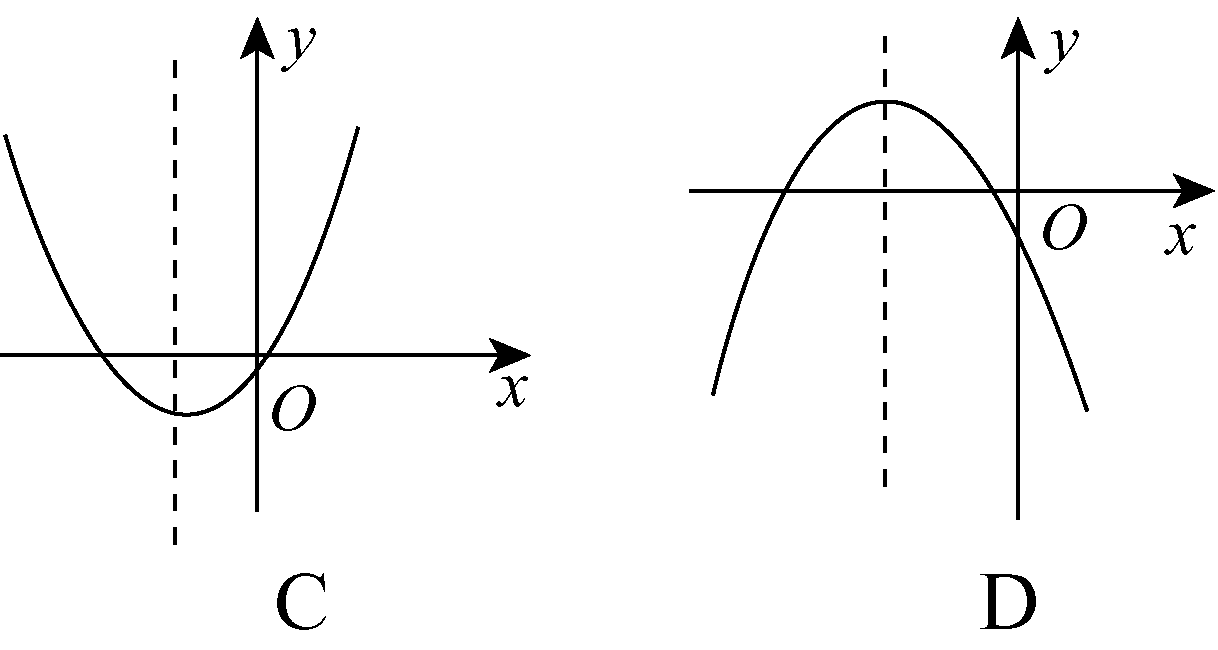
10.已知二次函数y=ax2+bx+c的图象如图4所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有( B )
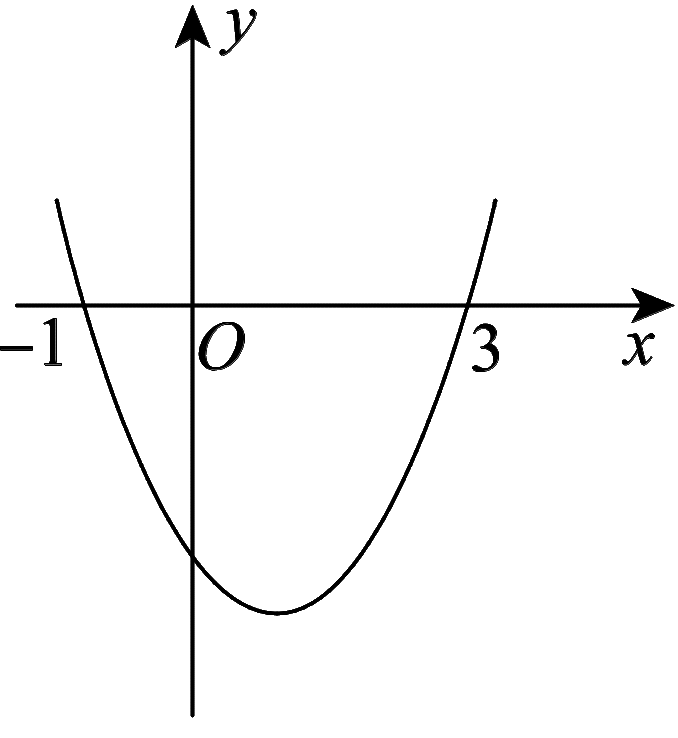
图4
A.3个 B.2个
C.1个 D.0个
二、填空题(每小题4分,共24分)
11.将二次函数y=x2-4x+5化为y=(x-h)2+k的形式,则__y=(x-2)2+1__.
12.抛物线y=2(x+1)2是由抛物线y=2x2向__左__平移__1__个单位得到的.
13.若二次函数y=(m+1)x2+m2-9的图象经过原点且有最大值,则m=__-![]() 3__.
3__.
【解析】 ∵二次函数的图象过原点,∴m2-9=0,解得m=3或m=-3,又∵m+1<0,∴m=-3.`
14.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为__y=-x2-4x-9__.
【解析】 设y=a(x+2)2-5,则a(1+2)2-5=-14,解得a=-1,所以y=-(x+2)2-5,即y=-x2-4x-9.
15.有一个抛物线形拱桥,其最大高度为16 m,跨度为40 m,现把它的示意图放在平面直角坐标系中如图5所示,则抛物线的解析式是__y=-x2+x__.
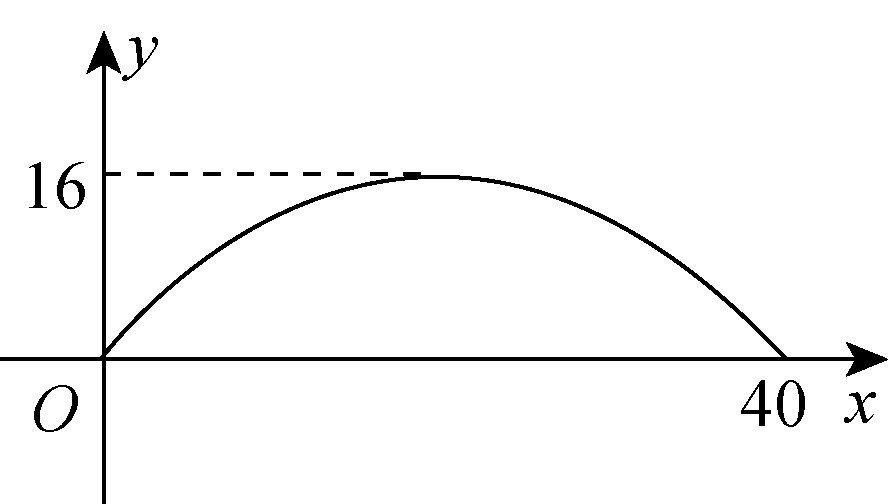
图5
【解析】 抛物线的顶点为(20,16),且过点(0,0),
设抛物线的解析式为y=a(x-20)2+16,
把(0,0)代入得a×400+16=0,a=-.
∴y=-(x-20)2+16,即y=-x2+x.
16.已知二次函数y=ax2+bx+c的图象交x轴于A,B两点,交y轴于C点,且△ABC是直角三角形,请写出符合要求的一个二次函数的解析式:__y=-x2+1__.
三、解答题(共66分)
17.(10分)通过配方,写出下列抛物线的开口方向、对称轴和顶点坐标.
(1)y=x2-3x-4;(2)y=-4x2+3x.
解:(1![]() )y=x2-3x-4=(x-)2-,开口向上,对称轴x=,顶点坐标为(,-);
)y=x2-3x-4=(x-)2-,开口向上,对称轴x=,顶点坐标为(,-);
(2)y=-4x2+3x=-4(x-)2+,开口向下,对称轴x=,顶点坐标为(,).
18.(8分)已知二次函数的图象经过点A(0,-3),![]() 且顶点P的坐标为(1,-4).
且顶点P的坐标为(1,-4).
(1)求这个函数的解析式;
(2)在平面直角坐标系中,画出它的图象.
解:(1)设二次函数的解析式为y=a(x-1)2-4,将点A(0,-3)代入,得-3=a(0-1)2-4,解得a=1,
∴y=(x-1)2-4,即y=x2-2x-3.
(2)如图所示:
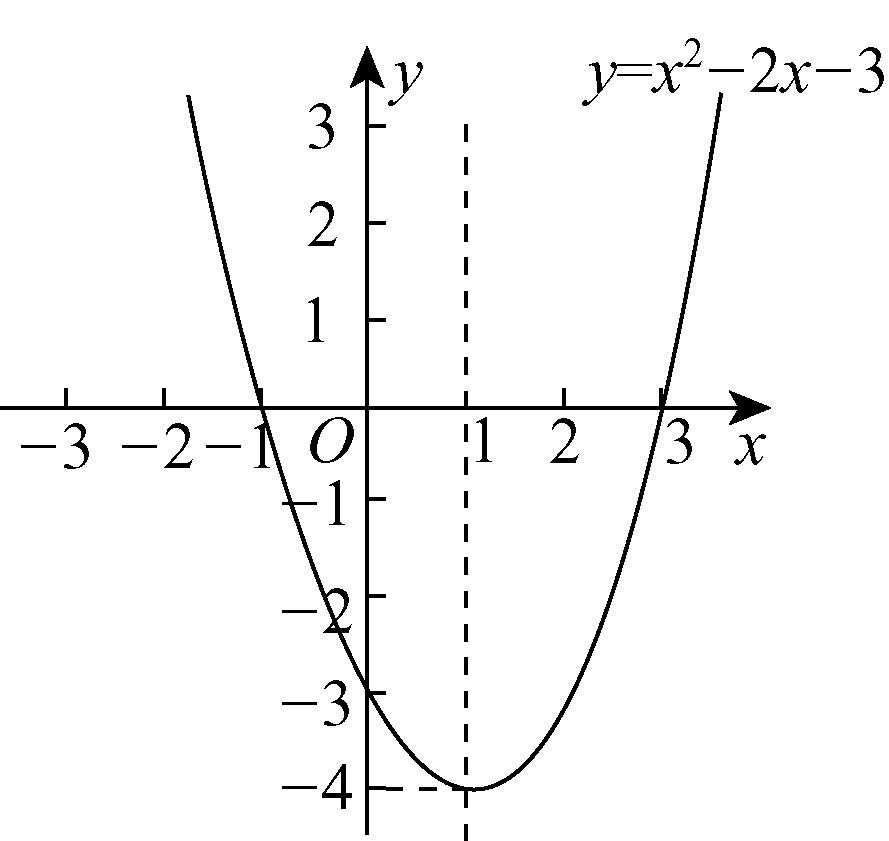
19.(8分)如图6,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.
(1)试确定b,c的值;
(2)过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点,试确定△M![]() CD的形状.
CD的形状.
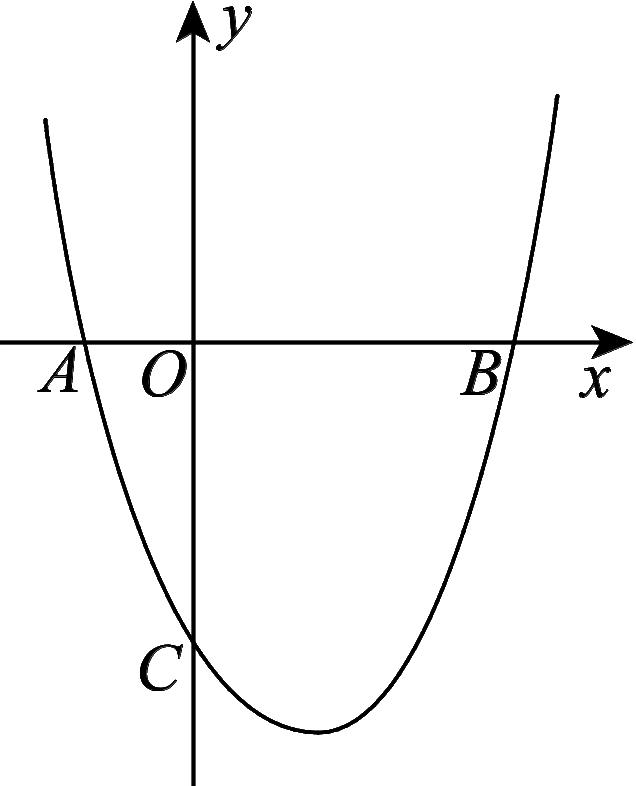
图![]() 6
6
解:(1)将A,B两点坐标代入二次函数的解析式,得
解得b=-2,c=-3.
(2)由(1)得二次函数的解析式为y=x2-2x-3,
配方得y=x2-2x+1-4
=(x-1)2-4,
抛物线的顶点M的坐标为(1,-4).
令x=0,得y=-3,所以C(0,-3).
由抛物线的对称性可得D(2,-3),CD=2,CM=DM=,因为CM2+DM2=CD2,
所以△MCD是等腰直角三角形.
20.(10分)某商人如果将进价为8元的商品按每件10元出售,每天可销售100件,现采用提高售价,减少进货量的办法增加利润,已知这种商品每涨价1元其销售量就要减少10件,问他将售价定为多少元时,才能使每天所赚的利润最大,并求出最大利润.
解:设将售价定为x元时,所赚利润为y元,
则y=[100-10(x-10)](x-8)
=(100-10x+100)(x-8)
=(200-10x)(x-8)
=-10x2+280x-1 600
=-10(x-14)2+360,
当x=14时,y取得最大值360,
故将售价定为14元时,才能使每天所赚的利润最大,最大利润为360元.
21.(10分)如图7,直线l经过A(3,0),B(0,3)两点,且与二次函数y=x2+1的图象在第一象限内相交于点C.求:
(1)△AOC的![]() 面积;
面积;
(2)二次函数图象的顶点D与点A,B组成的三角形的面积.
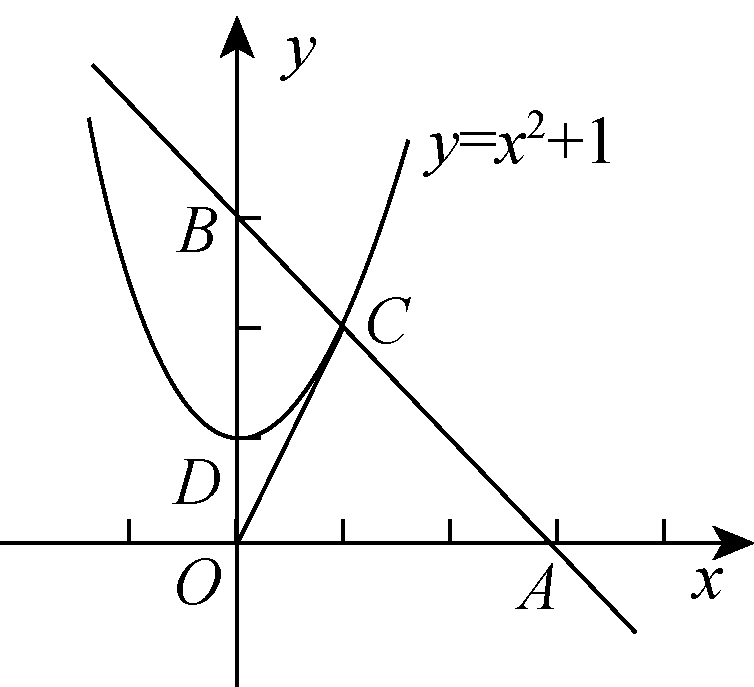
图7
解:(1)设过A,B两点的一次函数解析式为y=kx+b,
则解得
∴y=-x+3.
由
得或
又点C在第一象限内,∴C(1,2),
∴S△AOC=×OA×2=×3×2=3.
(2)∵D(0,1),
∴S△ABD=BD·OA=×(3-1)×3=3.
22.(10![]() 分)某工厂要赶制一批抗震救灾用的大型活动板房,如图8(1),板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12
m,抛物线拱高为5.6
m.
分)某工厂要赶制一批抗震救灾用的大型活动板房,如图8(1),板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12
m,抛物线拱高为5.6
m.
(1)在如图8(2)所示的平面直角坐标系中,求抛物线的解析式.
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5 m,高1.6 m,相邻窗户之间的间距均为0.8 m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8 m.请计算最多可安装几扇这样的窗户.

(1) (2)
图8
解:(1)设抛物线的解析式为y=ax2,
∵点B(6,-5.6)在抛物线上,
∴-5.6=36a,a=-,
∴抛物线的解析式为y=-x2.
(2)设窗户上边所在直线交抛物线于C,D两点,D点坐标为(k,t).
已知窗户高1.6 m,∴t=-5.6+1.6=-4,
∴-4=-k2,
解得k1≈5.07,k2≈-5.07,
∴CD=|k|×2=10.14(m).
又设最多可安装n扇窗户,则1.5n+0.8(n+1)≤10.14,
解得n≤4.06.
即最多可安装4扇窗户.
23.(10分)[2013·安顺]如图9,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于C(0,3).
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形,若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
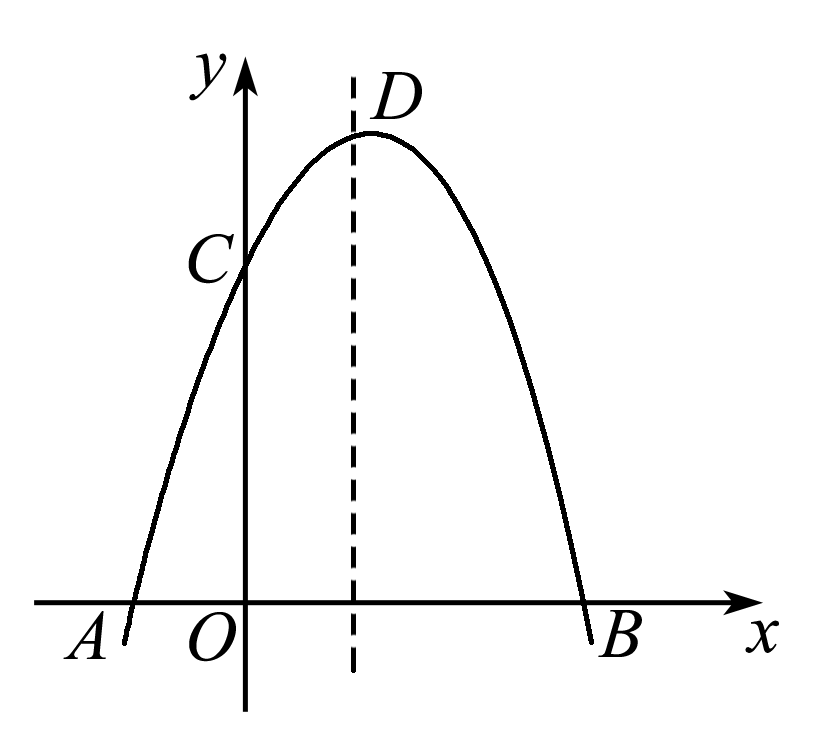
图9
解:(1![]() )∵抛物线与y轴交于点(0,3)
)∵抛物线与y轴交于点(0,3)
∴设抛物线的解析式为y=ax2+bx+3(a≠0)
根据题意,得,解得.
所以抛物线的解析式为y=-x2+2x+3.
(2)存在.
由y=-x2+2x+3,得D点的坐标为(1,4),对称轴为x![]() =1.
=1.
① 若以CD为底边,则PD=PC,
设P点的坐标为(x,y),根据勾股定理,得x2+(3-y)2=(x-1)2+(4-y)2,
即y=4-x.
又点P(x,y)在抛物线上,
∴4-x=-x2+2x+3,即x2-3x+1=0.解得x![]() =,
=,
∵<1,应舍去,
∴x=.
y=4-x=.即点P的坐标为(,).
② 若以CD为一腰,因为点P在对称轴右侧的抛物线上,由抛物线的对称性知,点P与点C关于直线x=1对称,此时点P的坐标为(2,3).
∴符合条件的点P的坐标为(,)或(2,3).