预习导航

1．连续函数

一般地，如果函数y＝f(x)在某个区间I上的图象是一条连续不断的曲线，那么就把它称为区间I上的连续函数．

2．曲边梯形的面积

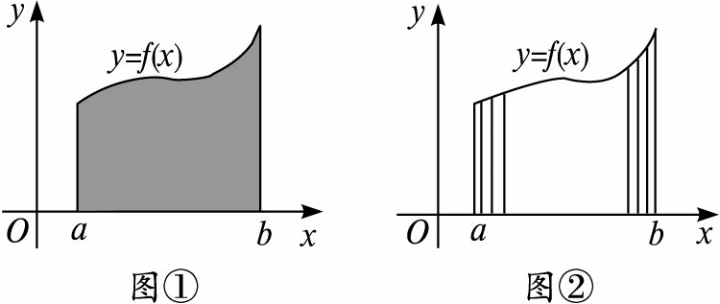
(1)曲边梯形：由直线x＝a，x＝b(a≠b)，y＝0和曲线y＝f(x)所围成的图形称为曲边梯形(如图①)．

(2)求曲边梯形面积的方法与步骤：

①分割：把区间[a，b]分成许多小区间，进而把曲边梯形拆分为一些小曲边梯形(如图②)；

②近似代替：对每个小曲边梯形“以直代曲”，即用矩形的面积近似代替小曲边梯形的面积，得到每个小曲边梯形面积的近似值(如图②)；

③求和：以近似代替得到的每个小曲边梯形面积的近似值求和；

④取极限：当小曲边梯形的个数趋向无穷时，各小曲边梯形的面积之和趋向一个定值，即为曲边梯形的面积．

3．变速直线运动的路程

一般地，如果物体做变速直线运动，速度函数为v＝v(t)，那么也可以采用分割、近似代替、求和、取极限的方法，求出它在a≤t≤b内的位移s.

本节中所说的“路程”在物理中的标准说法是“位移”．

思考1在求曲边梯形面积中第一步“分割”的目的是什么？

提示：“分割”的目的在于更精确的“以直代曲”，即以“矩形”代替“曲边梯形”．当然“分割”的越多，这种“代替”就越精确．

思考2求曲边梯形面积时，能否直接对整个曲边梯形进行“以直代曲”呢？怎样才能减小误差？

提示：不能直接对整个曲边梯形进行“以直代曲”，否则误差太大．为了减小近似代替的误差，需要先分割再分别对每个小曲边梯形“以直代曲”．