学业分层测评（五）

(建议用时：45分钟)

[学业达标]

一、选择题

1．不等式1<|x＋1|<3的解集为(　　)

A．(0,2) B．(－2,0)∪(2,4)

C．(－4,0) D.(－4，－2)∪(0,2)

【解析】　由1<|x＋1|<3，得

1<x＋1<3或－3<x＋1<－1，

∴0<x<2或－4<x<－2，

∴不等式的解集为(－4，－2)∪(0,2)．

【答案】　D

2．不等式>的解集是(　　)

A．(0,2) B．(－∞，0)

C．(2，＋∞) D.(－∞，0)∪(2，＋∞)

【解析】　由绝对值的意义知，>等价于<0，即x(x－2)<0，解得0<x<2.

【答案】　A

3．若不等式|ax＋2|＜6的解集为(－1,2)，则实数a的取值为(　　)

A．8 B．2

C．－4 D.－8

【解析】　原不等式化为－6＜ax＋2＜6，

即－8＜ax＜4.

又∵－1＜x＜2，∴验证选项易知a＝－4适合．

【答案】　C

4．若不等式|x＋1|＋|x－2|≥a的解集为R，则实数a的取值范围是(　　)

A．a≥3 B．a≤3

C．a＞3 D.a＜3

【解析】　令t＝|x＋1|＋|x－2|，由题意知

只要t_min≥a即可，

因为|x＋1|＋|x－2|≥|(x＋1)－(x－2)|＝3，所以t_min＝3，∴a≤3.

即实数a的取值范围是(－∞，3]，故选B.

【答案】　B

5．设集合A＝{x||x－a|<1，x∈R}，B＝{x||x－b|>2，x∈R}，若A⊆B，则实数a，b必满足(　　)

A．|a＋b|≤3 B．|a＋b|≥3

C．|a－b|≤3 D.|a－b|≥3

【解析】　由|x－a|<1，得a－1<x<a＋1.

由|x－b|>2，得x<b－2或x>b＋2.

∵A⊆B，∴a－1≥b＋2或a＋1≤b－2，

即a－b≥3或a－b≤－3，∴|a－b|≥3.

【答案】　D

二、填空题

6．不等式|x－5|－|x＋3|≥4的解集为________.

【导学号：32750023】

【解析】　当x<－3时，原不等式为8≥4恒成立；当－3≤x≤5时，原不等式为(5－x)－(x＋3)≥4，解得x≤－1，所以－3≤x≤－1；当x>5时，原不等式为(x－5)－(x＋3)≥4，无解．综上可知，不等式|x－5|－|x＋3|≥4的解集为{x|x≤－1}．

【答案】　{x|x≤－1}

7．若关于x的不等式|ax－2|<3的解集为，则a＝________.

【解析】　∵|ax－2|<3，∴－1<ax<5.

当a>0时，－<x<，与已知条件不符；

当a＝0时，x∈R，与已知条件不符；

当a<0时，<x<－.又不等式的解集为，故a＝－3.

【答案】　－3

8．若关于x的不等式|x＋2|＋|x－1|＜a的解集为∅，则a的取值范围为________．

【解析】　法一：由|x＋2|＋|x－1|＝|x＋2|＋|1－x|≥|x＋2＋1－x|＝3，知a≤3时，原不等式无解．

法二：数轴上任一点到－2与1的距离之和最小值为3.

所以当a≤3时，原不等式的解集为∅.

【答案】　(－∞，3]

三、解答题

9．已知关于x的不等式|x|＞ax＋1的解集为{x|x≤0}的子集，求a的取值范围．

【解】　设y₁＝|x|，y₂＝ax＋1.

则y₁＝

在同一直角坐标系中作出两函数图象，如图所示．

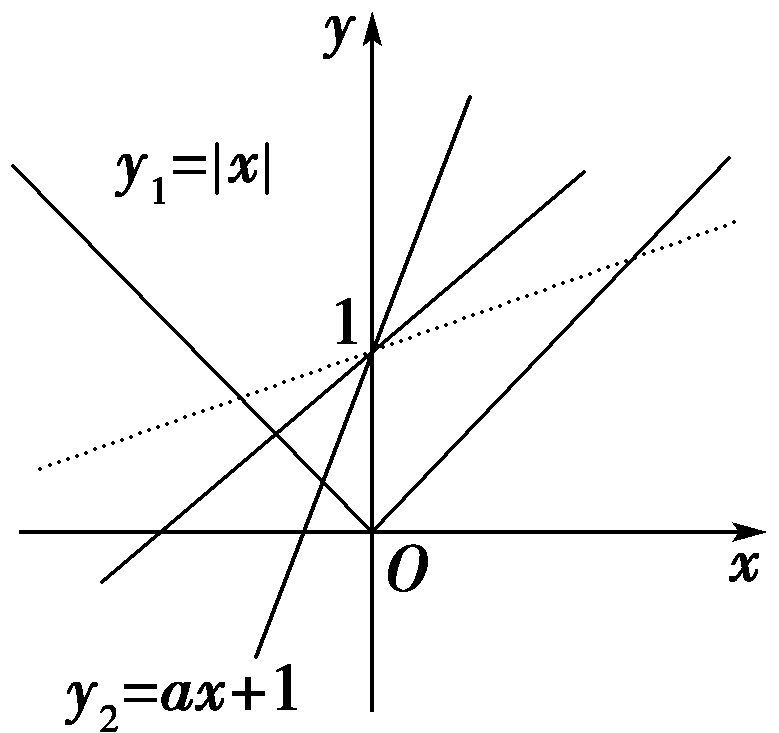
|x|＞ax＋1，只需考虑函数y₁＝|x|的图象位于y₂＝ax＋1的图象上方的部分，可知a≥1，即a的取值范围是[1，＋∞)．

10．已知函数f(x)＝|x－3|＋|x－2|＋k.

(1)若f(x)≥3恒成立，求k的取值范围；

(2)当k＝1时，求不等式f(x)<3x的解集．

【解】　(1)|x－3|＋|x－2|＋k≥3，对任意x∈R恒成立，即(|x－3|＋|x－2|)_min≥3－k.

又|x－3|＋|x－2|≥|x－3－x＋2|＝1，(|x－3|＋|x－2|)_min＝1≥3－k，解得k≥2.

(2)当x≤2时，5x>6，解得x>，∴<x≤2.

当2<x<3时，3x>2，解得x>，∴2<x<3.

当x≥3时，x>－4，∴x≥3.

综上，解集为.

[能力提升]

1．如果关于x的不等式|x－a|＋|x＋4|≥1的解集是全体实数，则实数a的取值范围是(　　)

A．(－∞，3]∪[5，＋∞)

B．[－5，－3]

C．[3,5]

D．(－∞，－5]∪[－3，＋∞)

【解析】　在数轴上，结合绝对值的几何意义可知a≤－5或a≥－3.

【答案】　D

2．若关于x的不等式|x＋1|≥kx恒成立，则实数k的取值范围是(　　)

A．(－∞，0] B．[－1,0]

C．[0,1] D.[0，＋∞)

【解析】　作出y＝|x＋1|与y＝kx的图象，如图，当k＜0时，直线一定经过第二、四象限，从图看出明显不恒成立；当k＝0时，直线为x轴，符合题意；当k＞0时，要使|x＋1|≥kx恒成立，只需k≤1.

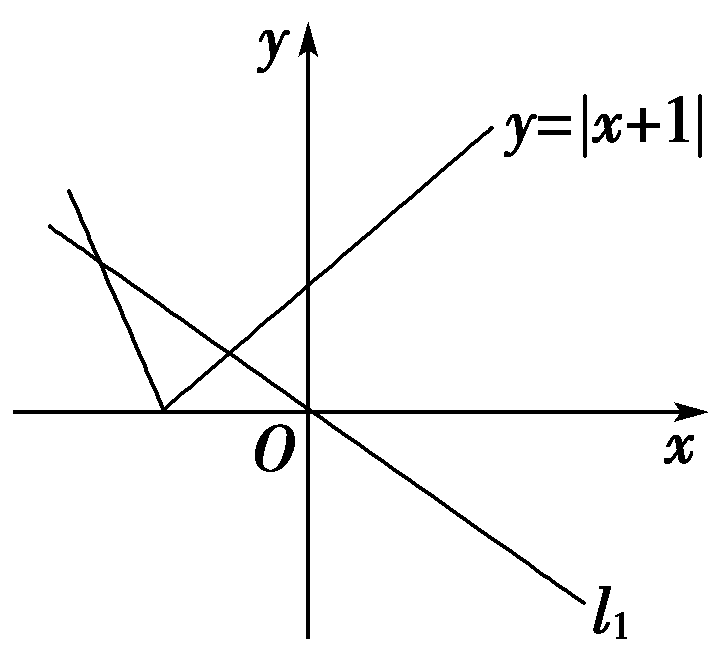
综上可知k∈[0,1]．

【答案】　C

3．若关于x的不等式|x－1|＋|x－a|≥a的解集为R(其中R是实数集)，则实数a的取值范围是________．

【解析】　不等式|x－1|＋|x－a|≥a恒成立，

a不大于|x－1|＋|x－a|的最小值，

∵|x－1|＋|x－a|≥|1－a|，

∴|1－a|≥a,1－a≥a或1－a≤－a，

解得a≤.

【答案】　

4．已知a∈R，设关于x的不等式|2x－a|＋|x＋3|≥2x＋4的解集为A.

(1)若a＝1，求A；

(2)若A＝R，求a的取值范围.

【导学号：32750024】

【解】　(1)当x≤－3时，原不等式化为－3x－2≥2x＋4，得x≤－3.

当－3＜x≤时，原不等式化为4－x≥2x＋4，得－3＜x≤0.

当x＞时，原不等式化为3x＋2≥2x＋4，得x≥2.

综上，A＝{x|x≤0或x≥2}．

(2)当x≤－2时，|2x－a|＋|x＋3|≥0≥2x＋4成立．

当x＞－2时，|2x－a|＋|x＋3|＝|2x－a|＋x＋3≥2x＋4，

得x≥a＋1或x≤，

所以a＋1≤－2或a＋1≤，得a≤－2.

综上，a的取值范围为(－∞，－2]．