第二十四章圆单元检测

一．填空题

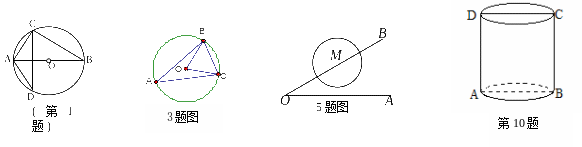
1 .如图，AB是⊙O的直径，若AB=4㎝，∠D=30°，则AC= ㎝.

2.已知⊙O的直径AB为2cm,那么以AB为底，第三个顶点在圆周上的三角形中，面积最大的三角形的面积等于 ㎝².

3. 如图,ΔABC是⊙O 的内接三角形，BC=4cm, ∠A=30°,则ΔOBC的面积为 cm².

4.已知矩形ABCD中，AB=6cm，AD=8cm，若以A为圆心作圆，使B、C、D三点中至少有一点在圆内，且至少有一点在圆外，则⊙A的半径r的取值范围是 .

5.如图，已知∠AOB=30°，M为OB边上一点，以M为圆心、2cm为半径作⊙M. 若点M在OB边上运动，则当OM= cm时，⊙M与OA相切.

6.两圆相切，圆心距为5，其中一个圆的半径为4，则另一个圆的半径为 .

7.在半径为10 cm的圆中，72°的圆心角所对的弧长为 cm.

8. 将一个弧长为12 cm, 半径为10cm的扇形铁皮围成一个圆锥形容器(不计接缝), 那么这个圆锥形容器的高为_____cm.

9．若圆锥侧面积是底面积的2倍，则这个圆锥的侧面展开图的圆心角是 .

1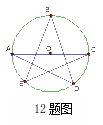 0．如图，已知圆柱体底面圆的半径为 ，高为2，AB、CD分别是两底面的直径，AD、BC是母线,若一只小虫从A点出发，从侧面爬行到C点，则小虫爬行的最短的路线的长度是 (结果保留根式)．

二．选择题

11.已知⊙O的半径为2cm, 弦AB的长为2 ，则这条弦的中点到弦所对优弧的中点的距离为（ ）

A.1cm B.3cm C.(2+ )cm D.(2+ )cm

12.如图，已知A、B、C、D、E均在⊙O上，且AC为直径，则∠A+∠B+∠C=（ ）度.

A．30 B．45 C．60 D．90

13.⊿ABC中，∠C=90°，AB=5，BC=4，以A为圆心，以3为半径，则点C与⊙A的位置关系为（ ）

A.点C在⊙A内 B.点C在⊙A上 C.点C在⊙A外 D.点C在⊙A上或点C在⊙A外

14.设⊙O的半径为r，圆心O到直线L的距离为d，若直线L与⊙O有交点，则d与r的关系为（ ）

A.d=r B.d<r C.d>r D.d≤r

15.以点P（1，2）为圆心，r为半径画圆，与坐标轴恰好有三个交点，则r应满足（ ）

A. r=2或 B. r=2 C. r= D. 2≤r≤

16.如图中的正方形的边长都相等，其中阴影部分面积相等的图形的个数是（ ）

A．1个 B．2个 C．3个 D．4个

17.一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B点从开始至结束所走过的路径长度为（ ）

A . B. C.4 D.2＋

1 8．如图，半径为2的两个等圆⊙O₁与⊙O₂外切于点P，过O₁作⊙O₂的两条切线，切点分别为A、B，与⊙O₁分别交于C、D，则APB与CPD的弧长之和为（ ）

A. B. C. D.

19．现有一圆心角为90°，半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为（ ）

A．4cm B．3cm C．2cm D．1cm

20.两个等圆⊙O₁和⊙O₂相交于A，B两点，且⊙O₁经过点O₂，则四边形O₁A O₂B是（ ）

A、两个邻边不相等的平行四边形 B、菱形 C、矩形 D、正方形

三、解答题

2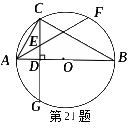 1．如图，⊙O是△ABC的外接圆，AB为直径，AC＝CF，CD⊥AB于D，且交⊙O于G，AF交CD于E．

（1）求∠ACB的度数；

（2）求证：AE＝CE；

2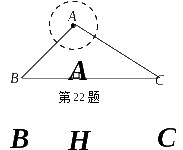 2．如图，点A是一个半径为300m的圆形森林公园的中心，在森林公园附近有B，C两个村庄，现要在B，C两村庄之间修一条长为1000m的笔直公路将两村连通，现测得∠ABC＝45°，∠ACB＝30°，问此公路是否会穿过该森林公园？并通过计算进行说明．

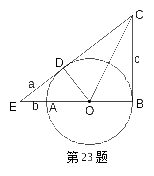
23．如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D，CE与BA的延长线交于点E,连结OC、OD．

（1）求证：△OBC≌△ODC；

（2）已知DE=a，AE=b，BC=c，请你思考后，选用以上适当的数，设计出计算⊙O半径r的一种方案：①你选用的已知数是 ；

1. 写出求解过程．（结果用字母表示）

2 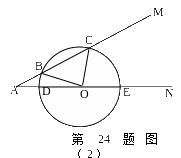4．已知：如图，∠MAN=30°，O为边AN上一点，以O为圆心、2为半径作⊙O，交AN于D、E两点，设AD= ，

⑴.如图⑴当 取何值时，⊙O与AM相切；

⑵.如图⑵当 为何值时，⊙O与AM相交于B、C两点，且∠BOC=90°．

25.如图中（1）、（2）、…（m）分别是边长均大于2的三角形、四边形、…、凸n边形.分别

以它们的各顶点为圆心，以1为半径画弧与两邻边相交，得到3条弧、4条弧……、n条弧.

⑴图⑴中3条弧的弧长的和为_________；

⑵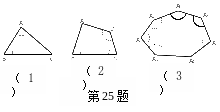 中4条弧的弧长的和为___________；

⑵求图(m)中n条弧的弧长的和 (用n表示).

26.在一次科学探究实验中，小明将半径为5cm的圆形滤纸片按图1所示的步骤进行折叠，并围成圆锥形.

(1)取一漏斗，上部的圆锥形内壁（忽略漏斗管口处）的母线OB长为6cm，开口圆的直径为6cm.当滤纸片重叠部分三层，且每层为 圆时，滤纸围成的圆锥形放入该漏斗中，能否紧贴此漏斗的内壁（忽略漏斗管口处），请你用所学的数学知识说明；

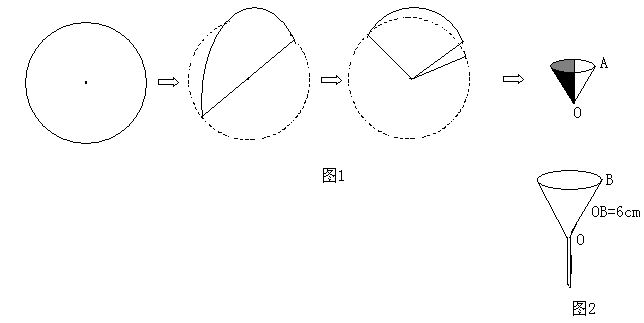( 2)假设有一特殊规格的漏斗，其母线长为6cm，开口圆的直径为7.2cm，现将同样大小的滤纸围成重叠部分为三层的圆锥形，放入此漏斗中，且能紧贴漏斗内壁.问重叠部分每层的面积为多少？

第二十四章 单元检测答案

一．填空题12999.com

1.2 2.1 3.4 4.6＜r＜10 5.4 6.1或9 7.4 8.8 9.180° 10.2

二．选择题

11.B 12.D 13.B 14.D 15.A 16.C 17.B 18.A 19.C 20.B

三.解答题

21.（1）90° （2）略

22.过A作AD⊥BC交BC于D.求得AD=500（ -1）＞300，所以此公路不会穿过该森林公园.

23.（1）略 （2）答案不唯一.现提供两例：一 .①a和b ②r= 二. ①a、b 、c ②r=

24.(1)x=2 (2)x=2 -2

25.(1) ;2 (2)(n-2)

26. (1) 通过计算得知滤纸围成的漏斗与真正的漏斗“展开”圆心角都是180°，所以能. (2)5

备注：已发表于07--08学年《学苑新报》第25期