A． B． C． D．
九年级（上）期中数学试卷
一、选择题（本大题共6小题，每小题3分，共18分．每小题只有一个正确选项）
1．下列汽车标志中，既是轴对称图形又是中心对称图形的是（ ）
A． B． C． D．
2．已知m是方程x2﹣x﹣2=0的一个根，则代数式m2﹣m+2的值等于（ ）
A．4 B．1 C．0 D．﹣1
3．已知点P关于x轴的对称点P1的坐标是（2，3），那么点P关于原点的对称点P2的坐标是（ ）
A．（﹣3，﹣2） B．（2，﹣3） C．（﹣2，﹣3） D．（﹣2，3）
4．抛物线y=（x+2）2﹣3可以由抛物线y=x2平移得到，则下列平移过程正确的是（ ）
A．先向左平移2个单位，再向上平移3个单位
B．先向左平移2个单位，再向下平移3个单位
C．先向右平移2个单位，再向下平移3个单位
D．先向右平移2个单位，再向上平移3个单位
5．已知关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，则k的取值范围是（ ）
A．k＜﹣2 B．k＜2 C．k＞2 D．k＜2且k≠1
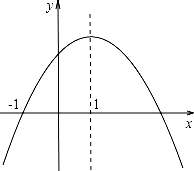
6．二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出下列结论：①b2﹣4ac＞0；②2a+b＜0；③4a﹣2b+c=0；④a：b：c=﹣1：2：3．其中正确的是（ ）
A．①② B．②③ C．③④ D．①④
二、填空题（本大题共8小题，每小题3分，共24分）
7．一元二次方程x2﹣3x=0的根是 ．
8．某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是 ．
9．我们在教材中已经学习了：①等边三角形；②矩形；③平行四边形；④等腰三角形；⑤菱形．在以上五种几何图形中，既是轴对称图形，又是中心对称图形的是 ．
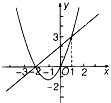
10．二次函数y=ax2+bx+c和一次函数y=mx+n的图象如图所示，则ax2+bx+c≤mx+n时，x的取值范围是 ．
11．方程x2﹣2x﹣k=0的一个实数根为3，则另一个根为 ．
12．已知二次函数y=（x﹣1）2+4，若y随x的增大而减小，则x的取值范围是 ．
13．已知抛物线y=x2﹣2（k+1）x+16的顶点在x轴上，则k的值是 ．
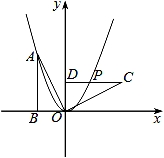
14．如图，Rt△OAB的顶点A（﹣2，4）在抛物线y=ax2上，将Rt△OAB绕点O顺时针旋转90°，得到△OCD，边CD与该抛物线交于点P，则点P的坐标为 ．
三、（本大题共4小题，每小题6分，共24分）
15．解方程：x（2x+3）=4x+6．
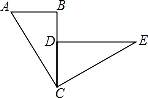
16．如图，已知：BC与CD重合，∠ABC=∠CDE=90°，△ABC≌△CDE，并且△CDE可由△ABC逆时针旋转而得到．请你利用尺规作出旋转中心O（保留作图痕迹，不写作法，注意最后用墨水笔加黑），并直接写出旋转角度是 ．
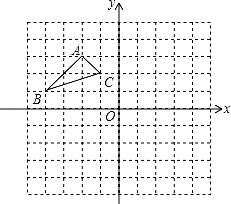
17．如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知△ABC．
（1）作出△ABC以O为旋转中心，顺时针旋转90°的△A1B1C1，（只画出图形）．
（2）作出△ABC关于原点O成中心对称的△A2B2C2，（只画出图形），写出B2和C2的坐标．
18．已知x1，x2是关于x的一元二次方程x2﹣6x+k=0的两个实数根，且x12x22﹣x1﹣x2=115．
（1）求k的值；
（2）求x12+x22+8的值．
四、（本大题共4小题，每小题8分，共32分）
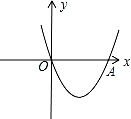
19．如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．
（1）求这个二次函数的解析式；
（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标．
20．已知等腰△ABC的一边长a=3，另两边长b、c恰好是关于x的方程x2﹣（k+2）x+2k=0的两个根，求△ABC的周长．
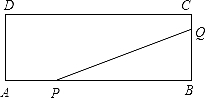
21．如图，矩形ABCD的两边长AB=18cm，AD=4cm，点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动，当一点到达终点时，另一点也停止运动．设运动时间为x秒，△PBQ的面积为y（cm2）．
（1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的最大值．
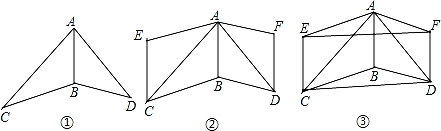
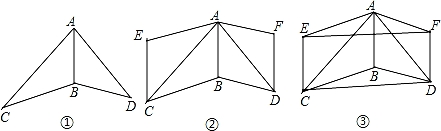
22．在同一平面内，△ABC和△ABD如图①放置，其中AB=BD．
小明做了如下操作：
将△ABC绕着边AC的中点旋转180°得到△CEA，将△ABD绕着边AD的中点旋转180°得到△DFA，如图②，请完成下列问题：
（1）试猜想四边形ABDF是什么特殊四边形，并说明理由；
（2）连接EF，CD，如图③，求证：四边形CDEF是平行四边形．
五、（本大题共10分）
23．如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系（如图1），y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．
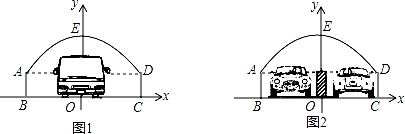
（1）求抛物线的解析式；
（2）现有一辆货运卡车，高4.4m，宽2.4m，它能通过该隧道吗？
（3）如果该隧道内设双向道（如图2），为了安全起见，在隧道正中间设有0.4m的隔离带，则该辆货运卡车还能通过隧道吗？
六、（本大题共12分）
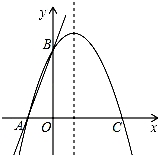
24．如图，直线y=3x+3交x轴于A点，交y轴于B点，过A、B两点的抛物线交x轴于另一点C（3，0）．
（1）求A、B的坐标；
（2）求抛物线的解析式；
（3）在抛物线的对称轴上求一点P，使得△PAB的周长最小，并求出最小值；
（4）在抛物线的对称轴上是否存在点Q，使△ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．
九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共6小题，每小题3分，共18分．每小题只有一个正确选项）
1．下列汽车标志中，既是轴对称图形又是中心对称图形的是（ ）
A． B． C． D．
【考点】中心对称图形；轴对称图形．
【分析】根据轴对称图形与中心对称图形的概念求解．
【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误；
B、既不是中心对称图形，也不是轴对称图形，故本选项错误；
C、不是轴对称图形，是中心对称图形，故本选项错误；
D、是中心对称图形，也是轴对称图形，故本选项正确．
故选D．
【点评】本题考查中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．
2．已知m是方程x2﹣x﹣2=0的一个根，则代数式m2﹣m+2的值等于（ ）
A．4 B．1 C．0 D．﹣1
【考点】一元二次方程的解．
【分析】把x=m代入方程x2﹣x﹣2=0求出m2﹣m=2，代入求出即可．
【解答】解：把x=m代入方程x2﹣x﹣2=0得：
m2﹣m﹣2=0，
m2﹣m=2，
所以m2﹣m+2=2+2=4．
故选A．
【点评】本题考查了一元二次方程的解，求代数式的值的应用，能求出m2﹣m=2是解此题的关键．
3．已知点P关于x轴的对称点P1的坐标是（2，3），那么点P关于原点的对称点P2的坐标是（ ）
A．（﹣3，﹣2） B．（2，﹣3） C．（﹣2，﹣3） D．（﹣2，3）
【考点】关于原点对称的点的坐标；关于x轴、y轴对称的点的坐标．
【分析】平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，﹣y），关于y轴的对称点的坐标是（﹣x，y），关于原点的对称点是（﹣x，﹣y）．
【解答】解：∵点P关于x轴的对称点P1的坐标是（2，3），
∴点P的坐标是（2，﹣3）．
∴点P关于原点的对称点P2的坐标是（﹣2，3）．故选D．
【点评】考查了平面内两个点关于坐标轴对称和原点对称的坐标关系．
4．抛物线y=（x+2）2﹣3可以由抛物线y=x2平移得到，则下列平移过程正确的是（ ）
A．先向左平移2个单位，再向上平移3个单位
B．先向左平移2个单位，再向下平移3个单位
C．先向右平移2个单位，再向下平移3个单位
D．先向右平移2个单位，再向上平移3个单位
【考点】二次函数图象与几何变换．
【分析】根据“左加右减，上加下减”的原则进行解答即可．
【解答】解：抛物线y=x2向左平移2个单位可得到抛物线y=（x+2）2，
抛物线y=（x+2）2，再向下平移3个单位即可得到抛物线y=（x+2）2﹣3．
故平移过程为：先向左平移2个单位，再向下平移3个单位．
故选：B．
【点评】本题考查的是二次函数的图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减．
5．已知关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，则k的取值范围是（ ）
A．k＜﹣2 B．k＜2 C．k＞2 D．k＜2且k≠1
【考点】根的判别式；一元二次方程的定义．
【专题】计算题；压轴题．
【分析】根据方程有两个不相等的实数根，得到根的判别式的值大于0列出关于k的不等式，求出不等式的解集即可得到k的范围．
【解答】解：根据题意得：△=b2﹣4ac=4﹣4（k﹣1）=8﹣4k＞0，且k﹣1≠0，
解得：k＜2，且k≠1．
故选：D．
【点评】此题考查了根的判别式，以及一元二次方程的定义，弄清题意是解本题的关键．
6．二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出下列结论：①b2﹣4ac＞0；②2a+b＜0；③4a﹣2b+c=0；④a：b：c=﹣1：2：3．其中正确的是（ ）
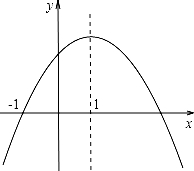
A．①② B．②③ C．③④ D．①④
【考点】二次函数图象与系数的关系．
【专题】计算题．
【分析】由二次函数图象与x轴有两个交点，得到根的判别式大于0，可得出选项①正确；由二次函数的对称轴为直线x=1，利用对称轴公式列出关系式，化简后得到2a+b=0（i），选项②错误；由﹣2对应的函数值为负数，故将x=﹣2代入抛物线解析式，得到4a﹣2b+c小于0，选项③错误；由﹣1对应的函数值等于0，将x=﹣1代入抛物线解析式，得到a﹣b+c=0（ii），联立（i）（ii），用a表示出b及c，可得出a：b：c的比值为﹣1：2：3，选项④正确，即可得到正确的选项．
【解答】解：由二次函数图象与x轴有两个交点，
∴b2﹣4ac＞0，选项①正确；
又对称轴为直线x=1，即﹣=1，
可得2a+b=0（i），选项②错误；
∵﹣2对应的函数值为负数，
∴当x=﹣2时，y=4a﹣2b+c＜0，选项③错误；
∵﹣1对应的函数值为0，
∴当x=﹣1时，y=a﹣b+c=0（ii），
联立（i）（ii）可得：b=﹣2a，c=﹣3a，
∴a：b：c=a：（﹣2a）：（﹣3a）=﹣1：2：3，选项④正确，
则正确的选项有：①④．
故选D
【点评】此题考查了二次函数图象与系数的关系，二次函数y=ax2+bx+c（a≠0），a的符合由抛物线的开口方向决定；c的符合由抛物线与y轴交点的位置确定；b的符合由对称轴的位置与a的符合决定；抛物线与x轴的交点个数决定了根的判别式的符合，此外还有注意二次函数图象上的一些特殊点，比如1，﹣1或2对应函数值的正负．
二、填空题（本大题共8小题，每小题3分，共24分）
7．一元二次方程x2﹣3x=0的根是 x1=0，x2=3 ．
【考点】解一元二次方程-因式分解法．
【专题】方程思想；因式分解．
【分析】首先利用提取公因式法分解因式，由此即可求出方程的解．
【解答】解：x2﹣3x=0，
x（x﹣3）=0，
∴x1=0，x2=3．
故答案为：x1=0，x2=3．
【点评】此题主要考查了因式分解法解一元二次方程，解题的关键会进行因式分解．
8．某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是 20% ．
【考点】一元二次方程的应用．
【专题】增长率问题．
【分析】设该药品平均每次降价的百分率为x，根据降价后的价格=降价前的价格（1﹣降价的百分率），则第一次降价后的价格是25（1﹣x），第二次后的价格是25（1﹣x）2，据此即可列方程求解．
【解答】解：设该药品平均每次降价的百分率为x，
由题意可知经过连续两次降价，现在售价每盒16元，
故25（1﹣x）2=16，
解得x=0.2或1.8（不合题意，舍去），
故该药品平均每次降价的百分率为20%．
【点评】本题考查数量平均变化率问题．原来的数量（价格）为a，平均每次增长或降低的百分率为x的话，经过第一次调整，就调整到a（1±x），再经过第二次调整就是a（1±x）（1±x）=a（1±x）2．增长用“+”，下降用“﹣”．
9．我们在教材中已经学习了：①等边三角形；②矩形；③平行四边形；④等腰三角形；⑤菱形．在以上五种几何图形中，既是轴对称图形，又是中心对称图形的是 ②⑤ ．
【考点】中心对称图形；轴对称图形．
【分析】根据中心对称图形以及轴对称图形的定义即可作出判断．
【解答】解：①等边三角形，是轴对称图形，不是中心对称图形，故选项错误；
②矩形，既是轴对称图形，又是中心对称图形，故选项正确；
③平行四边形，不是轴对称图形，是中心对称图形，故选项错误；
④等腰三角形，是轴对称图形，不是中心对称图形，故选项错误；
⑤菱形，既是轴对称图形，又是中心对称图形，故选项正确；
故答案为：②⑤．
【点评】本题主要考查了中心对称图形和轴对称图形的定义，正确理解定义是关键．
10．二次函数y=ax2+bx+c和一次函数y=mx+n的图象如图所示，则ax2+bx+c≤mx+n时，x的取值范围是 ﹣2≤x≤1 ．
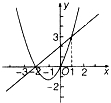
【考点】二次函数与不等式（组）．
【分析】求关于x的不等式ax2+bx+c≤mx+n的解集，实质上就是根据图象找出函数y=ax2+bx+c的值小于或等于y=mx+n的值时x的取值范围，由两个函数图象的交点及图象的位置，可求范围．
【解答】解：依题意得求关于x的不等式ax2+bx+c≤mx+n的解集，
实质上就是根据图象找出函数y=ax2+bx+c的值小于或等于y=mx+n的值时x的取值范围，
由两个函数图象的交点及图象的位置可以得到此时x的取值范围是﹣2≤x≤1．
故填空答案：﹣2≤x≤1．
【点评】解答此题的关键是把解不等式的问题转化为比较函数值大小的问题，然后结合两个函数图象的交点坐标解答，本题锻炼了学生数形结合的思想方法．
11．方程x2﹣2x﹣k=0的一个实数根为3，则另一个根为 ﹣1 ．
【考点】一元二次方程的解．
【分析】根据题意把3代入原方程求得k的值，然后把k的值代入原方程，从而解得原方程的两个根，即可求解．
【解答】解：∵方程x2﹣2x﹣k=0的一个实数根为3，
∴把3代入方程得：9﹣6﹣k=0，
∴k=3，
∴把k=3代入原方程得：x2﹣2x﹣3=0，
∴解得方程的两根分别为3和﹣1，
故答案为：﹣1．
【点评】本题主要考查了一元二次方程的解（根）的意义．解答本题的关键就是把3代入原方程求得k的值，然后再解得原方程的两个根．本题属于基础题比较简单．
12．已知二次函数y=（x﹣1）2+4，若y随x的增大而减小，则x的取值范围是 x≤1 ．
【考点】二次函数的性质．
【分析】根据二次函数的解析式的二次项系数判定该函数图象的开口方向、根据顶点式方程确定其图象的顶点坐标，从而知该二次函数的单调区间．
【解答】解：∵二次函数的解析式的二次项系数是，
∴该二次函数的开口方向是向上；
又∵该二次函数的图象的顶点坐标是（1，4），
∴该二次函数图象在[﹣∞1m]上是减函数，即y随x的增大而减小；
即：当x≤1时，y随x的增大而减小，
故答案为：x≤1．
【点评】本题考查了二次函数图象的性质．解答该题时，须熟知二次函数的系数与图象的关系、二次函数的顶点式方程y=（k﹣h）x2﹣b中的h，b的意义．
13．已知抛物线y=x2﹣2（k+1）x+16的顶点在x轴上，则k的值是 3或﹣5 ．
【考点】二次函数的性质．
【分析】抛物线y=ax2+bx+c的顶点纵坐标为，当抛物线的顶点在x轴上时，顶点纵坐标为0，解方程求k的值．
【解答】解：根据顶点纵坐标公式，
抛物线y=x2﹣2（k+1）x+16的顶点纵坐标为，
∵抛物线的顶点在x轴上时，
∴顶点纵坐标为0，即=0，
解得k=3或﹣5．
故本题答案为3或﹣5．
【点评】本题考查了二次函数的顶点坐标的运用．抛物线y=ax2+bx+c的顶点坐标为（﹣，）．
14．如图，Rt△OAB的顶点A（﹣2，4）在抛物线y=ax2上，将Rt△OAB绕点O顺时针旋转90°，得到△OCD，边CD与该抛物线交于点P，则点P的坐标为 （，2） ．
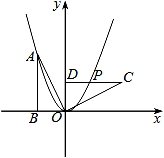
【考点】二次函数图象上点的坐标特征；坐标与图形变化-旋转．
【分析】先根据待定系数法求得抛物线的解析式，然后根据题意求得D（0，2），且DC∥x轴，从而求得P的纵坐标为2，代入求得的解析式即可求得P的坐标．
【解答】解：∵Rt△OAB的顶点A（﹣2，4）在抛物线y=ax2上，
∴4=4a，解得a=1，
∴抛物线为y=x2，
∵点A（﹣2，4），
∴B（﹣2，0），
∴OB=2，
∵将Rt△OAB绕点O顺时针旋转90°，得到△OCD，
∴D点在y轴上，且OD=OB=2，
∴D（0，2），
∵DC⊥OD，
∴DC∥x轴，
∴P点的纵坐标为2，
代入y=x2，得2=x2，
解得x=±，
∴P（，2）．
故答案为（，2）．
【点评】本题考查了待定系数法求二次函数的解析式，二次函数图象上点的坐标特征，根据题意求得P的纵坐标是解题的关键．
三、（本大题共4小题，每小题6分，共24分）
15．解方程：x（2x+3）=4x+6．
【考点】解一元二次方程-因式分解法．
【分析】先移项；然后提取公因式（2x+3）分解因式，利用因式分解法解方程．
【解答】解：x（2x+3）﹣2（2x+3）=0，
∴（2x+3）（x﹣2）=0，
∴2x+3=0或x﹣2=0，
∴x1=﹣，x2=2．
【点评】本题考查了解一元二次方程﹣﹣因式分解法．因式分解法解一元二次方程的思想就是把未知方程化成2个因式相乘等于0的形式，如（x﹣a）（x﹣b）=0的形式，这样就可直接得出方程的解为x﹣a=0或x﹣b=0，即x=a或x=b．注意“或”的数学含义，这里x1和x2就是“或”的关系，它表两个解中任意一个成立时方程成立，同时成立时，方程也成立．
16．如图，已知：BC与CD重合，∠ABC=∠CDE=90°，△ABC≌△CDE，并且△CDE可由△ABC逆时针旋转而得到．请你利用尺规作出旋转中心O（保留作图痕迹，不写作法，注意最后用墨水笔加黑），并直接写出旋转角度是 90° ．
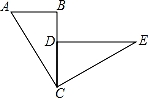
【考点】作图-旋转变换．
【专题】作图题．
【分析】分别作出AC，CE的垂直平分线进而得出其交点O，进而得出答案．
【解答】解：如图所示：旋转角度是90°．
故答案为：90°．
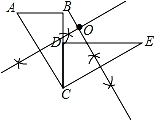
【点评】此题主要考查了旋转变换，得出旋转中心的位置是解题关键．
17．如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知△ABC．
（1）作出△ABC以O为旋转中心，顺时针旋转90°的△A1B1C1，（只画出图形）．
（2）作出△ABC关于原点O成中心对称的△A2B2C2，（只画出图形），写出B2和C2的坐标．
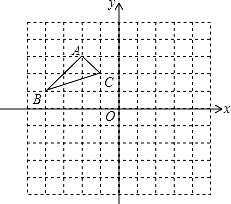
【考点】作图-旋转变换．
【专题】作图题．
【分析】（1）根据网格结构找出点A、B、C以O为旋转中心顺时针旋转90°后的对应点A1、B1、C1的位置，然后顺次连接即可；
（2）根据网格结构找出点A、B、C关于原点O成中心对称的点A2、B2、C2的位置，然后顺次连接即可，再根据平面直角坐标系写出B2和C2的坐标．
【解答】解：（1）△A1B1C1如图所示；
（2）△A2B2C2如图所示，
B2（4，﹣1），C2（1，﹣2）．
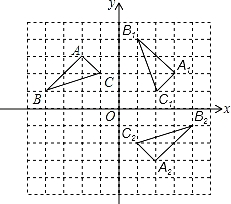
【点评】本题考查了利用旋转变换作图，熟练掌握网格结构准确找出对应点的位置是解题的关键．
18．已知x1，x2是关于x的一元二次方程x2﹣6x+k=0的两个实数根，且x12x22﹣x1﹣x2=115．
（1）求k的值；
（2）求x12+x22+8的值．
【考点】根与系数的关系；解一元二次方程-直接开平方法；根的判别式．
【专题】压轴题．
【分析】（1）方程有两个实数根，必须满足△=b2﹣4ac≥0，从而求出实数k的取值范围，再利用根与系数的关系，x12x22﹣x1﹣x2=115．即x12x22﹣（x1+x2）=115，即可得到关于k的方程，求出k的值．
（2）根据（1）即可求得x1+x2与x1x2的值，而x12+x22+8=（x1+x2）2﹣2x1x2+8即可求得式子的值．
【解答】解：（1）∵x1，x2是方程x2﹣6x+k=0的两个根，
∴x1+x2=6，x1x2=k，
∵x12x22﹣x1﹣x2=115，
∴k2﹣6=115，
解得k1=11，k2=﹣11，
当k1=11时，△=36﹣4k=36﹣44＜0，
∴k1=11不合题意
当k2=﹣11时，△=36﹣4k=36+44＞0，
∴k2=﹣11符合题意，
∴k的值为﹣11；
（2）∵x1+x2=6，x1x2=﹣11
∴x12+x22+8=（x1+x2）2﹣2x1x2+8=36+2×11+8=66．
【点评】总结：（1）一元二次方程根的情况与判别式△的关系：
①△＞0⇔方程有两个不相等的实数根；
②△=0⇔方程有两个相等的实数根；
③△＜0⇔方程没有实数根．
（2）根与系数的关系是：x1+x2=，x1x2=．
根据根与系数的关系把x12x22﹣x1﹣x2=115转化为关于k的方程，解得k的值是解决本题的关键．
四、（本大题共4小题，每小题8分，共32分）
19．如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．
（1）求这个二次函数的解析式；
（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标．
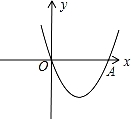
【考点】待定系数法求二次函数解析式；三角形的面积．
【分析】（1）直接把原点坐标代入y=x2+（2k﹣1）x+k+1求出k的值即可得到二次函数解析式；
（2）先确定A（3，0）和抛物线的对称轴，设B（x，x2﹣3x），再根据三角形面积公式得到•3•|x2﹣3x|=6，则x2﹣3x=4或x2﹣3x=﹣4，然后分别解方程求出x即可确定满足条件的B点坐标．
【解答】解：（1）把（0，0）代入得k+1=0，解得k=﹣1，
所以二次函数解析式为y=x2﹣3x；
（2）当y=0时，x2﹣3x=0，解得x1=0，x2=3，则A（3，0），
抛物线的对称轴为直线x=，
设B（x，x2﹣3x），
因为△AOB的面积等于6，
所以•3•|x2﹣3x|=6，
当x2﹣3x=4时，解得x1=﹣1，x2=4，则B点坐标为（4，4）；
当x2﹣3x=﹣4时，方程无实数解．
所以点B的坐标为（4，4）．
【点评】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．
20．已知等腰△ABC的一边长a=3，另两边长b、c恰好是关于x的方程x2﹣（k+2）x+2k=0的两个根，求△ABC的周长．
【考点】等腰三角形的性质；解一元二次方程-因式分解法．
【分析】先利用因式分解法求出两根：x1=2，x2=k．先分类讨论：若a=3为底边；若a=3为腰，分别确定b，c的值，求出三角形的周长．
【解答】解：x2﹣（k+2）x+2k=0
（x﹣2）（x﹣k）=0，
则x1=2，x2=k，
当b=c，
k=2，
则△ABC的周长=2+2+3=7，
当b=2，c=3或c=2，b=3
则k=3，
则△ABC的周长=2+3+3=8．
故△ABC的周长是7或8．
【点评】本题考查了解一元二次方程﹣因式分解法：先把方程右边变形为0，然后把方程左边进行因式分解，这样把一元二次方程转化为两个一元一次方程，再解一次方程可得到一元二次方程的解．也考查了解等腰三角形的性质．
21．如图，矩形ABCD的两边长AB=18cm，AD=4cm，点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动，当一点到达终点时，另一点也停止运动．设运动时间为x秒，△PBQ的面积为y（cm2）．
（1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的最大值．
【考点】矩形的性质；二次函数的最值．
【专题】动点型．
【分析】（1）分别表示出PB、BQ的长，然后根据三角形的面积公式列式整理即可得解；
（2）把函数关系式整理成顶点式解析式，然后根据二次函数的最值问题解答．
【解答】解：（1）∵S△PBQ=PB•BQ，PB=AB﹣AP=18﹣2x，BQ=x，
∴y=（18﹣2x）x，
即y=﹣x2+9x（0＜x≤4）；
（2）由（1）知：y=﹣x2+9x，
∴y=﹣（x﹣）2+，
∵当0＜x≤时，y随x的增大而增大，
而0＜x≤4，
∴当x=4时，y最大值=20，
即△PBQ的最大面积是20cm2．
【点评】本题考查了矩形的性质，二次函数的最值问题，根据题意表示出PB、BQ的长度是解题的关键．
22．在同一平面内，△ABC和△ABD如图①放置，其中AB=BD．
小明做了如下操作：
将△ABC绕着边AC的中点旋转180°得到△CEA，将△ABD绕着边AD的中点旋转180°得到△DFA，如图②，请完成下列问题：
（1）试猜想四边形ABDF是什么特殊四边形，并说明理由；
（2）连接EF，CD，如图③，求证：四边形CDEF是平行四边形．
【考点】旋转的性质；平行四边形的判定；菱形的判定．
【专题】几何综合题．
【分析】（1）根旋转的性质得AB=DF，BD=FA，由于AB=BD，所以AB=BD=DF=FA，则可根据菱形的判定方法得到四边形ABDF是菱形；
（2）由于四边形ABDF是菱形，则AB∥DF，且AB=DF，再根据旋转的性质易得四边形ABCE为平行四边形，根据平行四边形的性质得AB∥CE，且AB=CE，
所以CE∥FD，CE=FD，所以可判断四边形CDEF是平行四边形．
【解答】（1）解：四边形ABDF是菱形．理由如下：
∵△ABD绕着边AD的中点旋转180°得到△DFA，
∴AB=DF，BD=FA，
∵AB=BD，
∴AB=BD=DF=FA，
∴四边形ABDF是菱形；
（2）证明：∵四边形ABDF是菱形，
∴AB∥DF，且AB=DF，
∵△ABC绕着边AC的中点旋转180°得到△CEA，
∴AB=CE，BC=EA，
∴四边形ABCE为平行四边形，
∴AB∥CE，且AB=CE，
∴CE∥FD，CE=FD，
∴四边形CDEF是平行四边形．
【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了平行四边形的判定和菱形的判定．
五、（本大题共10分）
23．如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系（如图1），y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．
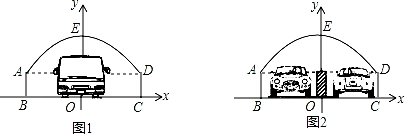
（1）求抛物线的解析式；
（2）现有一辆货运卡车，高4.4m，宽2.4m，它能通过该隧道吗？
（3）如果该隧道内设双向道（如图2），为了安全起见，在隧道正中间设有0.4m的隔离带，则该辆货运卡车还能通过隧道吗？
【考点】二次函数的应用．
【分析】（1）抛物线的解析式为y=ax2+c，根据E点及D点的坐标由待定系数法就可以求出结论；
（2）当y=2.4时代入（1）的解析式求出x的值就求出结论；
（3）将（2）求出的宽度﹣0.4m后除以2的值与2.4比较就可以求出结论．
【解答】解：（1）∵OE为线段BC的中垂线，
∴OC=BC．
∵四边形ABCD是矩形，
∴AD=BC=8m，AB=CD=2m，
∴OC=4．
∴D（4，2，）．E（0，6）．
设抛物线的解析式为y=ax2+c，由题意，得
，
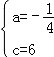解得：，
∴y=﹣x2+6；
（2）由题意，得
当y=4.4时，4.4=﹣x2+6，
解得：x=±，
∴宽度为：＞2.4，
∴它能通过该隧道；
（3）由题意，得
（﹣0.4）=﹣0.2＞2.4，
∴该辆货运卡车还能通过隧道．
【点评】本题考查了运用待定系数法求二次函数的解析式的运用，由函数值求自变量的值的运用，解答时求出二次函数的解析式是关键．
六、（本大题共12分）
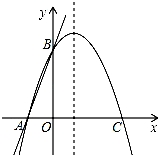
24．如图，直线y=3x+3交x轴于A点，交y轴于B点，过A、B两点的抛物线交x轴于另一点C（3，0）．
（1）求A、B的坐标；
（2）求抛物线的解析式；
（3）在抛物线的对称轴上求一点P，使得△PAB的周长最小，并求出最小值；
（4）在抛物线的对称轴上是否存在点Q，使△ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．
【考点】二次函数综合题．
【专题】综合题；二次函数图象及其性质．
【分析】（1）对于直线y=3x+3，分别令x与y为0求出对应y与x的值，确定出A与B坐标即可；
（2）根据A，C坐标，设出抛物线解析式，将C坐标代入即可确定出解析式；
（3）连接BC，与抛物线对称轴交于点P，连接AP，此时△PAB的周长最小，并求出最小值即可；
（4）在抛物线的对称轴上存在点Q，使△ABQ是等腰三角形，分四种情况考虑，求出满足题意Q坐标即可．
【解答】解：（1）对于直线y=3x+3，
令x=0，得到y=3；令y=0，得到x=﹣1，
则A（﹣1，0），B（0，3）；
（2）由A（﹣1，0），C（3，0），设抛物线解析式为y=a（x+1）（x﹣3），
把B（0，3）代入得：3=﹣3a，即a=﹣1，
则抛物线解析式为y=﹣（x+1）（x﹣3）=﹣x2+2x+3；
（3）连接BC，与抛物线对称轴交于点P，连接AP，由对称性得AP=CP，如图1所示，此时△ABP周长最小，
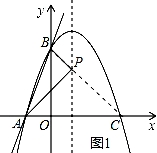
由抛物线解析式y=﹣x2+2x+3=﹣（x﹣1）2+4，得到对称轴为直线x=1，
设直线BC解析式为y=mx+n，
将B（0，3），C（3，0）代入得：，
解得：m=﹣1，n=3，即直线BC解析式为y=﹣x+3，
联立得：，
解得：，即P（1，2），
根据两点间的距离公式得：AB==，BC==3，
则P（1，2），周长为AB+BP+AP=AB+BP+PC=AB+BC=3+；
（4）在抛物线的对称轴上存在点Q，使△ABQ是等腰三角形，
如图2所示，分四种情况考虑：
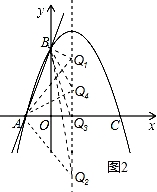
当AB=AQ1==时，
在Rt△AQ1Q3中，AQ3=2，AQ1=，
根据勾股定理得：Q1Q3==，此时Q1（1，）；
由对称性可得Q2（1，）；
当AB=BQ3时，可得OQ3=OA=1，此时Q3（1，0）；
当AQ4=BQ4时，Q4为线段AB垂直平分线与对称轴的交点，
∵A（﹣1，0），B（0，3），
∴直线AB斜率为=3，中点坐标为（﹣，），
∴线段AB垂直平分线方程为y﹣=﹣（x+），
令x=1，得到y=1，此时Q4（1，1），
综上，Q的坐标为（1，）或（1，﹣）或（1，0）或（1，1）．
【点评】此题属于二次函数综合题，涉及的知识有：坐标与图形性质，待定系数法确定二次函数解析式，待定系数法确定一次函数解析式，一次函数与坐标轴的交点，等腰三角形的性质，线段垂直平分线定理，勾股定理，以及对称的性质，熟练掌握性质及定理是解本题的关键．