七年级(上)期末目标检测数学试卷（五）

一、精心选一选（每题2分，共20分）

1．在跳远测试中，及格的标准是4.00米，王菲跳出了4.12米，记为＋0.12米，何叶跳出了3.95米，记作( )

A.＋0.05米 B.－0.05米 C.＋3.95米 D.－3.95米

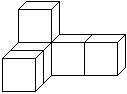
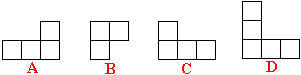
2．用大小一样的正方体搭一几何体(左图), 该几何体的左视图是右图中的（ ）

3．小红家分了一套住房，她想在自己的房间的墙上钉一根细木条，挂上自己喜欢的装饰物，那么小红至少需要几根钉子使细木条固定( )

A.1根 B.2根 C.3根 D.4根

4．下列各式中运算正确的是（ ）

A. B. C. D.

5．我国是一个严重缺水的国家，大家应倍加珍惜水资源，节约用水。据测试，拧不紧的水龙头每秒钟会滴下2滴水，每滴水约0.05毫升。若每天用水时间按2小时计算，那么一天中的另外22小时水龙头都在不断的滴水. 请计算，一个拧不紧的水龙头，一个月(按30天计算)浪费水（ ）

A. 23760毫升 B. 2.376×10⁵毫升 C. 23.8×10⁴毫升 D. 237.6×10³毫升

6 ．某同学解方程5 －1＝　 ＋3时，把 处数字看错得 ，他把　　处看成了（　 　）

Ａ．3　　　　　 Ｂ．－9　　　　 Ｃ．8　　　　　　 Ｄ．－8

7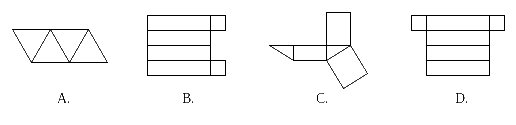 ．下列展开图中，不能围成几何体的是（ ）

8．关于 的方程 和 有相同的解，则 的值是（ ）

A. －8 B. 10 C. －10 D. 8

9．某商场有两件进价不同上衣均卖了80元，一件盈利60%，另一件亏本20%，这次买卖中商家（　 　）

Ａ．不赔不赚　　 Ｂ．赚了８元　　 Ｃ．赚了10元　　 Ｄ．赚了32元

10．一列数：0，1，2，3，6，7，14，15，30，__ __,_____,____这串数是由小明按照一定规则写下来的，他第一次写下“0，1”,第二次按着写“2，3”,第三次接着写“6，7”第四次接着写“14，15”，就这样一直接着往下写，那么这串数的最后三个数应该是下面的（ ）

A．31，32，64 B．31，62，63 C．31，32，33 D．31，45，46

二、细心填一填（每题3分，共30分）

11．我市12月中旬的一天中午气温为5℃，晚6时气温下降了8℃，则晚6时气温为______。

12．数轴上点A表示的数是 4，点B表示的数是3，那么AB＝__________。

13．12.42º= º ′ ″。

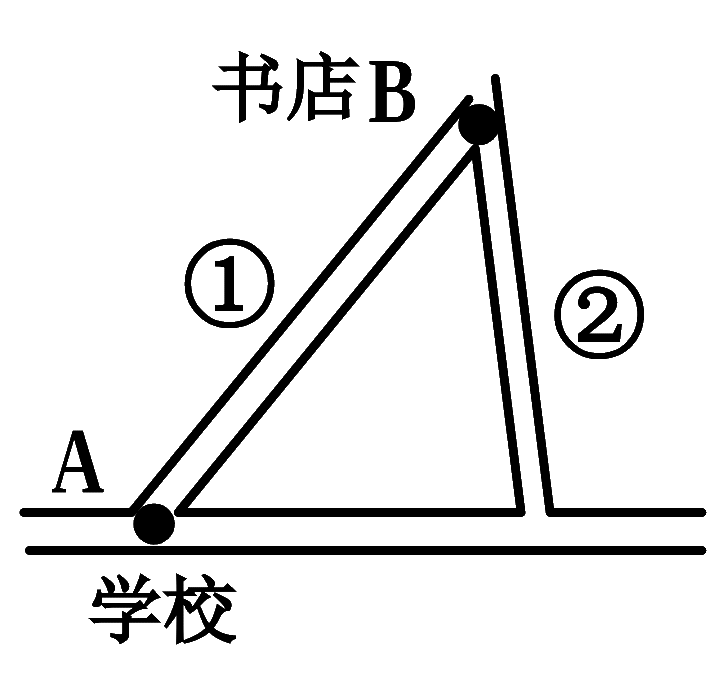
14．如图，从学校A到书店B最近的路线是①号路线，其道理用几何知识解释应是________________。

图1

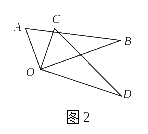
15．将两块直角三角板的直角顶点重合，如图所示，若∠AOD＝128°，则∠BOC＝ ___________-度。

16．已知 ，则方程 的解为__________。

17．火车从A地到B地途经C、D、E、F四个车站，且相邻两站之间的距离各不相同，则售票员应准备 种票价的车票.

18．麦迪在一次比赛中22投14中得28分，除了3个三分球全中外，他还投中了 两分球和 个罚球。

19．小明同学在上楼梯时发现：若只有一个台阶时，有一种走法；若有二个台阶时，可以一阶一阶地上，或者一步上二个台阶，共有两种走法；如果他一步只能上一个或者两个台阶，根据上述规律，有三个台阶时，他有三种走法，那么有四个台阶时，共有 种走法。

20．用“数字牌”做24点游戏，抽出的四张牌分别表示2、－3、－4、6（每张牌只能用一次，可以用加、减、乘、除等运算）请写出一个算式，使运算结果为24： .

三、用心解一解（本大题共70分）

21．（8分）计算：

（1） ； （2） .

22．（8分）解方程： .

23．（8分）先化简，再求值： ，其中 ， .

2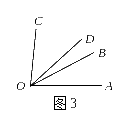 4．（8分）如图3，已知∠BOC ＝2∠AOB，OD平分∠AOC，∠BOD＝14°，求∠AOB的度数。

25．（10分）如图4，点C在线段AB上，AC＝8 cm，CB＝6 cm，点M、N分别是AC、BC的中点。

（1）求线段MN的长；

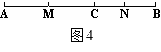（ 2）若C为线段AB上任一点，满足AC＋CB＝ cm，其它条件不变，你能猜想MN的长度吗？并说明理由。

26．（12分）在平整的地面上，有若干个完全相同的棱长为10cm的小正方体堆成一个几何体，如图4所示.（1）这个几何体由 个小正方体组成，请画出这个几何体的三视图.

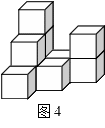
主视图 左视图 俯视图

（2）如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有 个正方体只有一个面是黄色，有 个正方体只有两个面是黄色，有 个正方体只有三个面是黄色.

（3）若现在你手头还有一些相同的小正方体，如果保持俯视图和左视图不变，最多可以再添加几个小正方体.这时如果要重新给这个几何体表面喷上红漆，需要喷漆的面积比原几何体增加还是减少了？增加或减少了多少cm²？

27．（16分）某中学组织七年级学生秋游，由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜.

（1）两同学向公司经理了解租车的价格.公司经理对他们说：“公司有45座和60座两种型号的客车可供租用，60座的客车每辆每天的租金比45座的贵100元.”王老师说：“我们学校八年级昨天在这个公司租了2辆60座和5辆45座的客车，一天的租金为1600元，你们能知道45座和60座的客车每辆每天的租金各是多少元吗？”甲、乙两同学想了一下，都说知道了价格.

你知道45座和60座的客车每辆每天的租金各是多少元？

（2）公司经理问：“你们准备怎样租车？”，甲同学说：“我的方案是只租用45座的客车，可是会有一辆客车空出30个座位”；乙同学说“我的方案只租用60座客车，正好坐满且比甲同学的方案少用两辆客车”，王老师在一旁听了他们的谈话说：“从经济角度考虑，还有别的方案吗？”如果是你，你该如何设计租车方案，并说明理由.

参考答案

一、1.B 2.C 3.B 4.D 5.B 6.C 7.B 8.A 9.C 10.B

二、11. －3℃ 12.7 13. 12º25′12″ 14. 两点之间，线段最短 15.52

16. 17.15 18.8，3 19. 5 20．答案不惟一，如 等

三、21. （1）解：原式＝ ＝ ＝0；

（2）解：原式＝ ＝18－20＝－2.

22. 解：去分母，得

去括号，得

移项，得

合并同类项，得

系数化为1，得

23．解：原式

当 ， 时，原式 .

24. 解：设 ,则

∵

∴

∴

即 。

25. 解：（1）∵点M、N分别是AC、BC的中点，

∴CM＝ AC＝4cm，CN＝ BC＝3 cm，∴MN＝CM＋CN＝4＋3＝7 cm；

（2）同（1）可得CM＝ AC ，CN＝ BC，

∴MN＝CM＋CN＝ AC＋ BC＝ （AC＋BC）＝ 。

26．解：（1）10，

（2）1，2，3；

（3）最多可以再添加4个小正方体，原几何体需喷32个面，新几何体需喷36个面，所以需喷漆的面积增加了，增加了4×10×10＝400 cm².

27．解：（1）设45座的客车每辆每天的租金为 元，

则60座的客车每辆每天的租金为( ＋100)元，

由题意，得2( ＋100)＋5 ＝1600.

解得 ＝200.

所以 ＋100＝200＋100＝3

即45座的客车每辆每天的租金是200元，60座的客车每辆每天的租金是300元.

（2）设租用45座的客车 辆，则租用60座的客车( －2)辆，

由题意，得45 －30＝60( －2).

解得 ＝6.

所以 －2＝4(辆).

所以该校七年级共有45×6－30＝240(人).

甲同学的方案需付租金：200×6＝1200(元)，

乙同学的方案需付租金：4×300＝1200(元)，

我的方案是：由上可知该校共有240人，可租用45座的客车4辆，租用60座的客车1辆，需付租金200×4＋300＝1100(元).