预习导航

课程目标

学习脉络

1．了解函数极值的概念，会从几何直观理解函数的极值与导数的关系，并会灵活应用．

2．掌握函数极值的判定及求法．

3．掌握函数在某一点取得极值的条件.


1．极值点与极值

(1)极小值点与极小值．

如图，函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则把点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．

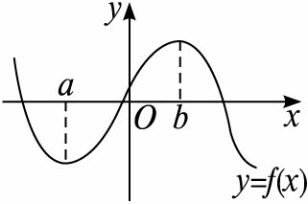
(2)极大值点与极大值．

如图，函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；而且在点x＝b附近的左侧f′(x)＞0，右侧f′(x)＜0，则把点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．

(3)极值的定义

①极大值和极小值统称为极值；极大值点和极小值点统称为极值点．

②极值反映了函数在某一点附近的大小情况，刻画的是函数的局部性质．

思考1(1)导数为0的点一定是函数的极值点吗？

(2)一个函数在一个区间的端点处可以取得极值吗？

(3)一个函数在给定的区间上是否一定有极值？若有极值，是否可以有多个？极大值一定比极小值大吗？

提示：(1)不一定，例如对于函数f(x)＝x3，虽有f′(0)＝0，但x＝0并不是f(x)＝x3的极值点，要使导数为0的点成为极值点，还必须满足其他条件．

(2)不可以，函数在一个区间的端点处一定不可能取得极值，因为不符合极值点的定义．

(3)在一个给定的区间上，函数可能有若干个极值点，也可能不存在极值点；函数可以只有极大值，没有极小值，或者只有极小值没有极大值，也可能既有极大值，又有极小值．极大值不一定比极小值大，极小值也不一定比极大值小．

思考2函数的极值与单调性有什么联系？

提示：极值点两侧单调性必须相反，若f(x)在区间(a，b)内有极值，那么f(x)在(a，b)内一定不是单调函数，即在区间上单调的函数没有极值．

2．求函数y＝f(x)的极值的方法

解方程f′(x)＝0，当f′(x0)＝0时：

(1)如果在x0附近的左侧f′(x)＞0，右侧f′(x)＜0，那么f(x0)是极大值；

(2)如果在x0附近的左侧f′(x)＜0，右侧f′(x)＞0，那么f(x0)是极小值．