2．如与的乘积中不含的一次项，则的值为（
）2016－2017学年八年级数学上册第三次月考模拟试卷
（测试时间120分钟 总分120分）
一、选择题（本题共6小题，每小题3分，共18分）
1．下列计算正确的是（ ）
A．m3+m3=m6 B．m3•m2=m6 C．（m3）2=m5 D．m3÷m2=m
2．如与的乘积中不含的一次项，则的值为（
）
A．
B．0
C．
1 D．
3
3．已知等腰三角形的两边长是5cm和6cm，则此三角形的周长是（ ）
A．16cm B．17cm C．11cm D．16cm或17cm
4．一个三角形的两边长分别为3和7，且第三边长为整数，这样的三角形的周长最小值是( )
A．14 B．15 C．16 D．17
5．若的值是（
）
A. 1 B. 25 C. 2 D. -10
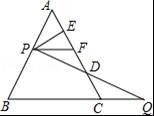
6．如图，已知等边△ABC和等边△PAF，过P作PE⊥AC于E，Q为BC延长线上一点，连接PQ交AC边于D，当PA=CQ，AB=1时，DE的长（ ）
A．
B．
C．
D．不能确定
二、填空题（本题共6小题，每小题3分，共18分）
7．已知a+b=3，ab=2，则a2b+ab2= ．
8．多项式+mx+25恰好是另一个多项式的平方，则m=_________
9．已知x、y是实数，并且
，则的值是_________
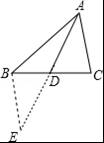
10．三角形ABC中，AD是中线，且AB=4，AC=6，求AD的取值范围是 ．
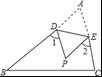
11．如图，将纸片△ABC沿DE折叠，点A落在点P处，已知 ∠1+∠2=100°，则∠A的大小等
于 度
12．如图，已知△ABC的内角∠A=°，分别作内角∠ABC与外角∠ACD的平分线，两条平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…以此类推得到∠A2014，则∠A2014的度数是
.
三、解答题（本大题共5小题，每小题6分，共30分）
13．因式分解
（1）
（2）
14．利用乘法公式计算：
（1）
（2）
15．一个多边形的外角和是内角和的，求这个多边形的边数．
16．先化简，再求值：（2a+b）2+5a（a+b）﹣（3a﹣b）2，其中a=3，b=．
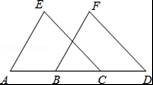
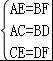
17．已知：如图，AB=DC，AE=BF，CE=DF，∠A=60°．
（1）求∠FBD的度数． （2）求证：EC∥DF．
18．在三个整式+2xy、+2xy、中，请你任意选出两个进行加（或减）运算，使所得整式可以因式分解，并进行因式分解．
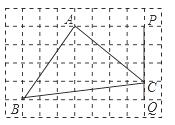
19．如图，方格纸中每个小正方形的边长均为1，线段AB和PQ的端点均在小正方形的顶点上．
（1）在线段PQ上确定一点C（点C在小正方形的顶点上）．使△ABC是轴对称图形，并在网格中画出△ABC；
（2）请直接写出△ABC的周长和面积．
20．如图，效果家门口的商店在装修，他发现工人正在一块半径为R的圆形板材上，冲去半径为r的四个小圆，小刚测得R=6.8cm，r=1.6cm，他想知道剩余阴影部分的面积，你能帮助小刚利用所学过的因式分解计算吗？请写出利用因式分解的求解的过程（π取3）
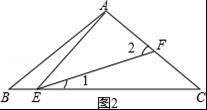
21．如图，在△ABC中，AB=AC，点E为BC边上一动点（不与点B、C重合），过点E作射线EF交AC于点F，使∠AEF=∠B．
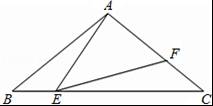
（1）判断∠BAE与∠CEF的大小关系，并说明理由；
（2）请你探索：当△AEF为直角三角形时，求∠AEF与∠BAE的数量关系．
22．对于任何实数，我们规定符号=ad﹣bc，例如：
=1×4﹣2×3=﹣2
（1）按照这个规律请你计算的值；
（2）按照这个规定请你计算，当a2﹣3a+1=0时，求的值．
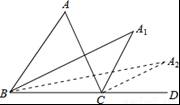
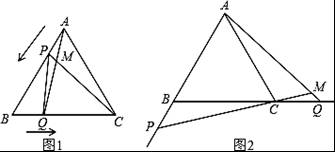
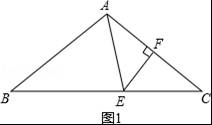
23．如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．
（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．
2016－2017学年八年级数学上册第三次月考模拟试卷
参考答案
1.D
2．A
【解析】
试题分析：根据多项式的乘法计算法则可得：(x+m)(x+3)=+(m+3)x+3m，根据乘积中不含x的一次项可得：m+3=0，则m=－3.
3．D
【解析】
试题分析：当5为腰长时，则等腰三角形的周长为：5×2+6=16cm；当6为腰长时，则等腰三角形的周长为：6×2+5=17cm.
4．B
【解析】
试题分析：根据三角形三边关系可得：7－3＜第三边＜7+3，即4＜第三边＜10，根据第三边为整数，则第三边最小值值为5，则周长为：3+7+5=15.
5．B
【解析】
试题分析：根据完全平方公式可得：－2mn=49－24=25.
6．B
【解析】解：∵△ABC是等边三角形，且PF∥BC，
又∵PE⊥AF，
∴AE=EF=AF；（等边三角形三线合一）
∵PF∥CQ，
∴∠PFD=∠QCD，∠FPD=∠Q；
又∵PA=PF=CQ，
在△PFD和△QCD中，
∴△PFD≌△QCD（AAS）；
∴CD=DF=CF；
∴DE=DF+FE=（AF+FC）=AC=，
故选B．
7．6
【解析】
试题分析：∵a+b=3，ab=2，
∴a2b+ab2=ab（a+b）=6．
故答案为：6．
8．±10
【解析】
试题分析：完全平方公式是指：，则m=±2×1×5=±10.
9．-1
【解析】
试题分析：几个非负数之和为零，则每个非负数都为零.根据题意可得：=0，=0，解得：x=，y=3，则原式==-1.
10．1＜AD＜5
【解析】解：延长AD到E，使AD=DE，连接BE，
1＜AD＜5
11．50
【解析】
试题分析：根据∠1+∠2=100°可得∠ADP+∠AEP=360°－100°=260°，根据折叠图形的性质可得：∠ADE+∠AED=260°÷2=130°，则∠A=180°－130°=50°.
12．
【解析】
试题分析：∵∠ACD是△ABC的外角，
∴∠ACD＝∠A＋∠ABC，
∵平分∠ABC，平分∠ACD，
∴，，
∵是的外角，
∴，
∴，
∴，
同理可得：，
根据规律可得：
13．(1)、(4+9)(2m+3)(2m－3)；(2)、4a
【解析】
试题分析：(1)、本题需要利用两次平方差公式进行因式分解；(2)、首先进行提取公因式4a，然后再利用完全平方公式进行因式分解.
试题解析：(1)、原式=(4+9)(4－9)=(4+9)(2m+3)(2m－3)
(2)、原式=4a()=4a
14．(1)、-8xy+9；(2)、
【解析】
试题分析：(1)、根据完全平方公式和多项式的乘法计算法则求出各式的值，然后进行求和得出答案；(2)、将a-2b看作一个整体，然后利用平方差公式和完全平方公式进行化简.
试题解析：(1)、原式=
(2)、原式=
15．9
【解析】
试题分析：首先设这个多边形的边数为n，然后根据定理列出方程，从而求出n的值.
试题解析：设这个多边形的边数为n，
依题意得：（n﹣2）180°=360°，
解得n=9．
答：这个多边形的边数为9．
16．﹣30
【解析】
试题分析：先算乘法，再合并同类项，最后代入求出即可．
解：（2a+b）2+5a（a+b）﹣（3a﹣b）2
=4a2+4ab+b2+5a2+5ab﹣9a2+6ab﹣b2
=15ab，
当a=3，b=﹣时，原式=15×3×（﹣）=﹣30．
点评：本题考查了整式的混合运算和求值的应用，主要考查学生的化简能力和计算能力，题目比较好，难度适中．
17．(1)、60°；(2)、证明过程见解析
【解析】
试题分析：(1)、根据AB=CD得出AC=BD，然后证明出△AEC和△BFD全等，从而得出答案；(2)、根据全等得出∠ACE=∠BDF，从而说明平行.
试题解析：(1)、∵AB=CD，∴AB+BC=CD+BC， ∴AC=BD，
在△AEC和△BFD中
∵△AEC≌△BFD， ∴∠A=∠FBD， ∵∠A=60°，∴∠FBD=60°；
(2)、∵△AEC≌△BFD， ∴∠ACE=∠BDF，∴EC∥DF．
18．(x+y)(x－y)
【解析】
试题分析：选择第一个和第二个进行做差，然后利用平方差公式进行因式分解.
试题解析：+2xy－(+2xy)=－=(x+y)(x－y)
19．(1)、答案见解析；(2)、周长为：10+5，面积为12.5
【解析】
试题分析：(1)、根据轴对称图形的性质得出点C；(2)、根据勾股定理分别求出三角形三边的长度，从而得出三角形的周长和面积.
试题解析：(1)、如图所示：△ABC即为所求；
(2)、△ABC的周长为：5+5+5=10+5，
面积为：7×4﹣×3×4﹣×3×4﹣×1×7=12.5．
20．108
【解析】
试题分析：用大圆的面积减去4个小圆的面积即可得到剩余阴影部分的面积，分解因式然后把R和r的值代入计算出对应的代数式的值．
解：阴影部分面积=πR2﹣4πr2
=π（R2﹣4r2）
=π（R﹣2r）（R+2r）
=3×﹙6.8+2×1.6﹚×﹙6.8﹣2×1.6﹚
=108．
21．（1）∠BAE=∠FEC（2）2∠AEF与∠BAE的数量关系是互余
【解析】
试题分析：（1）根据三角形内角与外角的关系可得∠B+∠BAE=∠AEC=∠AEF+∠FEC，再由条件∠AEF=∠B可得∠BAE=∠FEC；
（2）分别根据当∠AFE=90°时，以及当∠EAF=90°时利用外角的性质得出即可．
解：（1）∠BAE=∠FEC；
理由如下：
∵∠B+∠BAE=∠AEC，∠AEF=∠B，
∴∠BAE=∠FEC；
（2）如图1，当∠AFE=90°时，
∵∠B+∠BAE=∠AEF+∠CEF，
∠B=∠AEF=∠C，
∴∠BAE=∠CEF，
∵∠C+∠CEF=90°，
∴∠BAE+∠AEF=90°，
即∠AEF与∠BAE的数量关系是互余；
如图2，当∠EAF=90°时，
∵∠B+∠BAE=∠AEF+∠1，
∠B=∠AEF=∠C，
∴∠BAE=∠1，
∵∠C+∠1+∠AEF=90°，
∴2∠AEF+∠1=90°，
即2∠AEF与∠BAE的数量关系是互余．
【点评】此题考查了等腰三角形的性质以及外角的性质，此题难度适中，注意掌握分类讨论思想的应用．
22．（1）﹣22；（2）1
【解析】
试题分析：（1）根据已知展开，再求出即可；
（2）根据已知展开，再算乘法，合并同类项，变形后代入求出即可．
解：（1）原式=﹣2×5﹣3×4=﹣22；
（2）原式=（a+1）（a﹣1）﹣3a（a﹣2）
=a2﹣1﹣3a2+6a
=﹣2a2+6a﹣1，
∵a2﹣3a+1=0，
∴a2﹣3a=﹣1，
∴原式=﹣2（a2﹣3a）﹣1=﹣2×（﹣1）﹣1=1．
23．(1)、证明过程见解析；(2)、∠QMC=60°；(3)、∠QMC=120°.
【解析】
试题分析：(1)、根据等边三角形可得∠ABQ=∠CAP，AB=CA，根据速度相同可得AP=BQ，从而得出三角形全等；(2)、根据△ABQ≌△CAP得出∠BAQ=∠ACP，然后根据∠QMC=∠BAQ+∠MACC=∠BAC得出答案；(3)、根据△ABQ≌△CAP得出∠BAQ=∠ACP，然后根据∠QMC=∠ACP+∠APM=180°-∠PAC得出答案.
试题解析：(1)、∵△ABC是等边三角形
∴∠ABQ=∠CAP，AB=CA，
又∵点P、Q运动速度相同，
∴AP=BQ，
在△ABQ与△CAP中，AB=AC，∠ABQ=∠CAP，AP=BQ
∴△ABQ≌△CAP（SAS）；