

2017—2018学年度上学期高三年级第一调考试
数学理科试卷
第Ⅰ卷
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、设集合![]() ,若
,若![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、已知![]() 是虚数单位,若复数
是虚数单位,若复数![]() 为纯虚数,则实数
为纯虚数,则实数![]() 的值是
的值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
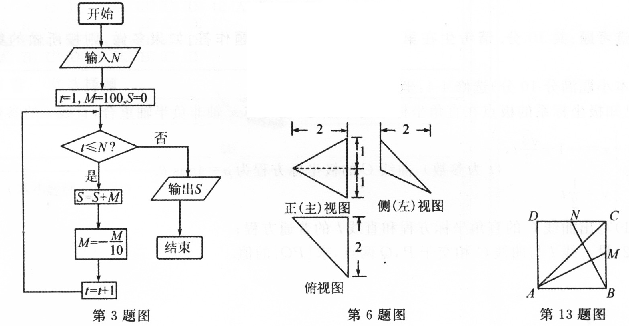
3、执行如图所示的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为
A.5 B.4 C.5 D.2
4、已知点![]() ,点
,点![]() 为平面区域
为平面区域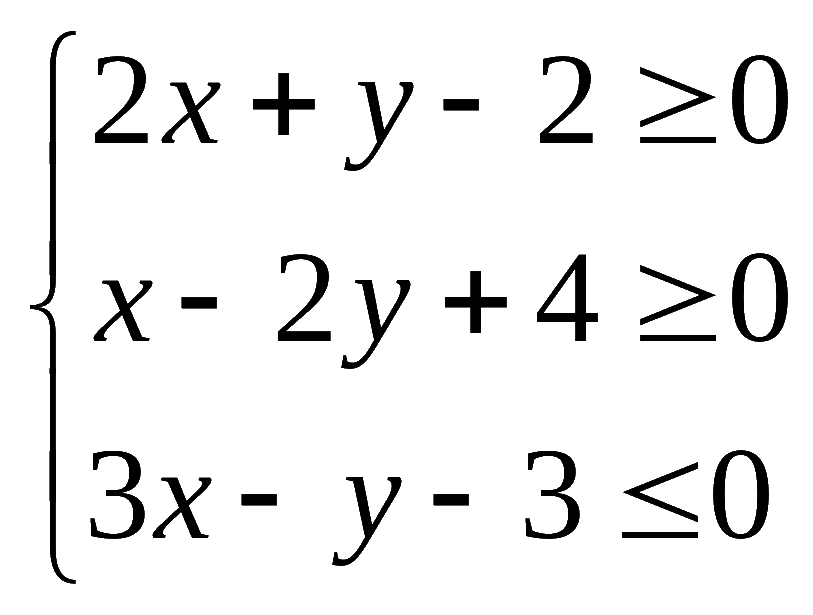 上的一个动点,则
上的一个动点,则![]() 的最小值是
的最小值是
A.5
B.3
C.![]() D.
D.![]()
5、已知![]() 的三个内角
的三个内角![]() 依次成等差数列,BC边上的中线
依次成等差数列,BC边上的中线![]() ,则
,则![]()
A.3
B.![]() C.
C.![]() D.
D.![]()
6、一个几何体的三视图如图所示,则该几何体的所有棱中,最长的棱长为
A.3
B.![]() C.
C.![]() D.
D.![]()
7、已知数列![]() 满足
满足 ,则
,则![]()
A.0
B.![]() C.
C.![]() D.
D.![]()
8、已知![]() ,函数
,函数![]() 在
在![]() 内单调递减,则
内单调递减,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、设函数![]() ,其中
,其中![]() ,若
,若![]() ,且
,且![]() 的最小正周期大于
的最小正周期大于![]() ,则
,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、已知函数![]() ,若实数
,若实数![]() 满足
满足![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、已知函数![]() 的图象的一对称中心的横坐标为
的图象的一对称中心的横坐标为![]() ,且
,且![]() 有三个零点,则实数
有三个零点,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、定义在内的函数满足:①当![]() 时,
时,![]() ;②
;②![]() (
(![]() 为正常数),若函数的所有极大值点都在同一直线上,则常数
为正常数),若函数的所有极大值点都在同一直线上,则常数![]() 的值是
的值是
A.1
B.![]() C.
C.![]() 或3
D.1或2
或3
D.1或2
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。.
13、如图,正方形ABCD中,M、N分别是BC、CD的中点,若![]() ,则
,则![]()
14、已知定义在实数集R上的函数![]() 满足
满足![]() ,且
,且![]() 的导函数
的导函数![]() ,
,
则不等式![]() 的解集为
的解集为
15、已知数列![]() 的前n项和
的前n项和![]() ,且成等比数列,
,且成等比数列,![]() 成等差数列,则
成等差数列,则![]() 等于
等于
16、已知函数![]() 是定义域为R的偶函数,当
是定义域为R的偶函数,当![]() 时,
时,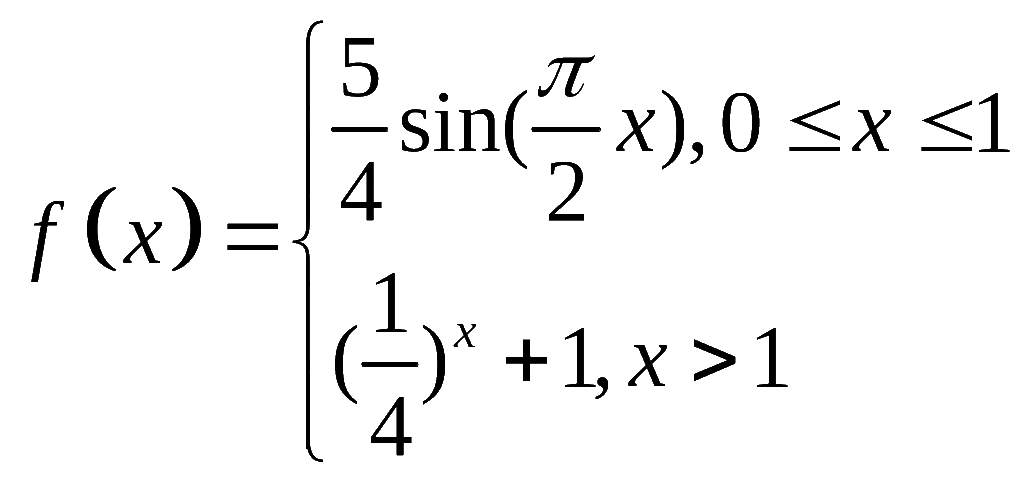 若关于
若关于![]() 的方程
的方程![]() 有且仅有6个不同的实数根,则实数
有且仅有6个不同的实数根,则实数![]() 的取值范围是
的取值范围是
三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤
(一)必考题:共60分
17、(本小题满分10分)
在![]() 中,角
中,角![]() 的对边分别是
的对边分别是![]() ,且
,且![]() 。
。
(1)求角A的大小;
(2)求![]() 的取值范围。
的取值范围。
18、(本小题满分12分)
高三某班12月月考语文成绩服从正态分布![]() ,数学成绩的频率分布直方图如图,如果成绩大于135分,则认为特别优秀。
,数学成绩的频率分布直方图如图,如果成绩大于135分,则认为特别优秀。
(1)这500名学生中本次考试语文、数学特别优秀的大约各多少人?
(2)如果语文和数学两科都特别优秀的共有6人,从(1)中的这些同学随机抽取3人,设三人中两科都特别优秀的有X人,求X的分布列和数学期望。
参考数据:若![]() ,则
,则![]() 。
。

19、(本小题满分12分)
如图①,在平行四边形![]() 中,
中,![]() 分别为
分别为![]() 的中点,现把平行四边形
的中点,现把平行四边形![]() 沿折起,如图②所示,连接
沿折起,如图②所示,连接![]() 。
。
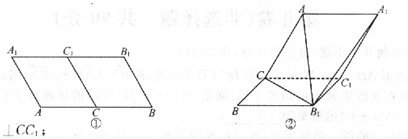
(1)求证:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
20、(本小题满分12分)
已知曲线![]() 在点
在点![]() 处的切线是
处的切线是![]() 。
。
(1)求实数![]() 的值;
的值;
(2)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的最大值。
的最大值。
21、(本小题满分12分)
已知函数![]() 为常数,
为常数,![]() )
)
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 在
在![]() 处取得极值时,若关于
处取得极值时,若关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不同的相等的实数根,求实数
上恰有两个不同的相等的实数根,求实数![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B铅笔在答题卡上把所选题目的题号涂黑,把答案填在答题卡上.
22、(本小题满分10分) 选修4-4 坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与x轴非负半轴重合,直线![]() 的参数方程为
的参数方程为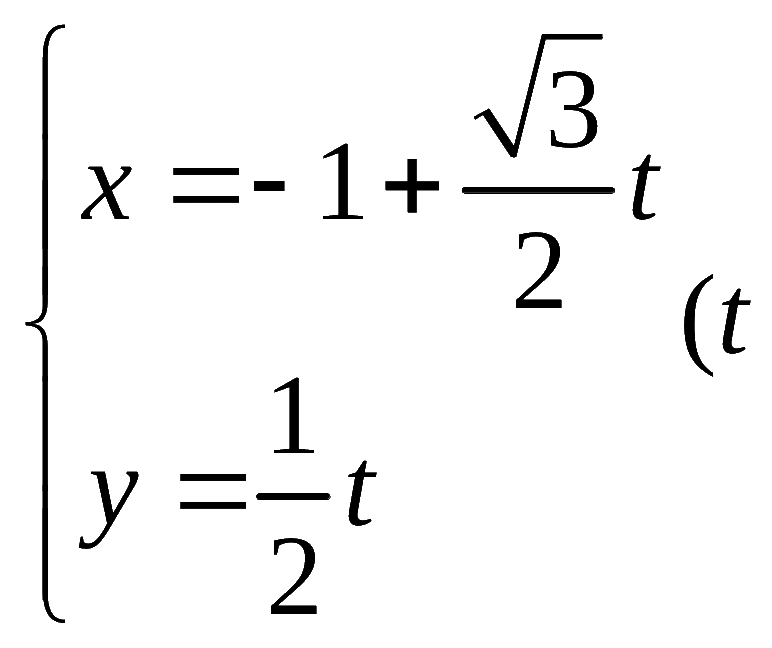 为参数),曲线C的极坐标方程为
为参数),曲线C的极坐标方程为![]() 。
。
(1)写出曲线C的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线C相交于
与曲线C相交于![]() 两点,求
两点,求![]() 的值。
的值。
23、(本小题满分10分))选修4-5 不等式选讲
已知函数![]() 。
。
(1)解不等式![]() ;
;
(2)若对于任意![]() ,都有
,都有![]() ,使得成立,求实数
,使得成立,求实数![]() 的取值范围。
的取值范围。



