3.2.1几类不同增长的函数模型

班级:__________姓名:__________设计人__________日期__________

课后练习

【基础过关】

1．在我国大西北，某地区荒漠化土地面积每年平均比上年增长10.4%，专家预测经过 年可能增长到原来的 倍，则函数 的图象大致为

2．当x越来越大时,下列函数中,增长速度最快的是(　　)

3．某商品价格前两年每年递增20%,后两年每年递减20%,则四年后的价格与原来的价格相比,变化情况是 (　　)

4．已知函数y₁=2^x,y₂=x²,y₃=log₂x,则当2<x<4时,有(　　)

5．假设某商品靠广告销售的收入 与广告费 之间满足关系 ，那么广告效应D ，当             时，取得最大广告效应，此时收入            .

6．四个变量 ， ， ， 随变量 变化的数据如下表：

关于 呈指数型函数变化的变量是          .

7．试比较函数y=x²⁰⁰,y=e^x,y=lg x的增长差异.

8．有一种树木栽植五年后可成材.在栽植后五年内,年增长20%,如果不砍伐,从第六年到第十年,年增长10%,现有两种砍伐方案:

甲方案:栽植五年后不砍伐,等到十年后砍伐.

乙方案:栽植五年后砍伐重栽,再过五年再砍伐一次.

请计算后回答:十年后哪一个方案可以得到较多的木材?(不考虑最初的树苗成本,只按成材的树木计算)

【能力提升】

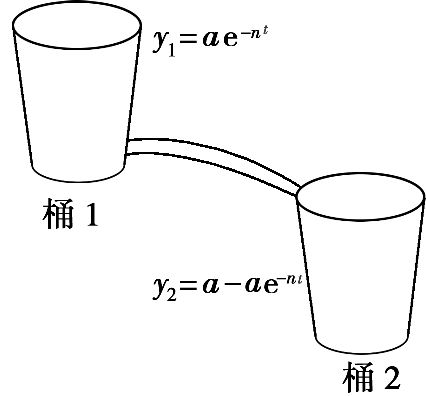
已知桶1与桶2通过水管相连如图所示,开始时桶1中有a L水,t min后剩余的水符合指数衰减函数y₁=a·e^-nt,那么桶2中的水就是y₂=a-a·e^-nt,假定5 min后,桶1中的水与桶2中的水相等,那么再过多长时间桶1中的水只有  L?

答案

【基础过关】

1．D

【解析】由已知可推断函数模型为指数函数.

2．D

【解析】由于指数函数的增长是爆炸式增长,则当x越来越大时,函数y=100^x的增长速度最快.

3．B

【解析】设该商品原价为a,则四年后的价格为a(1+20%)²(1-20%)²=0.921 6a,所以(1-0.921 6)a=0.078 4a=7.84%a,即四年后的价格比原来的价格减少了7.84%.

4．B

【解析】在同一平面直角坐标系内画出这三个函数的图象(图略),在区间(2,4)内,从上到下图象依次对应的函数为y₂=x²,y₁=2^x,y₃=log₂x,故y₂>y₁>y₃.

5． 　

【解析】 ，

∴ ，即 时，D最大.

此时 .

6．

【解析】由于指数函数的增长呈“爆炸式”，结合表中数据可知，关于x呈指数型函数变化的变量是 .

7．增长最慢的是y=lg x,由图象(图略)可知随着x的增大,它几乎平行于x轴.当x较小时,y=x²⁰⁰要比y=e^x增长得快;当x较大(如x>1 000)时,y=e^x要比y=x²⁰⁰增长得快.

8．设最初栽植量为a,甲方案在10年后木材产量为y₁=a(1+20%)⁵(1+10%)⁵=a(1.1×1.2)⁵≈4a.

乙方案在10年后木材产量为y₂=2a(1+20%)⁵=2a·1.2⁵≈4.98a.

∴y₁-y₂=4a-4.98a<0,则y₁<y₂.

因此,十年后乙方案可以得到较多的木材.

【能力提升】

由题意,得a·e^-5n=a-a·e^-5n,即e^-5n= 　①.

设再过t min桶1中的水只有  L,则a·e^-n(t+5)= a,即e^-n(t+5)= 　②.

将①式两边平方得e^-10n= 　③,

比较②,③得-n(t+5)=-10n,∴t=5.

即再过5 min桶1中的水只有  L.