2016年山东省高考数学试卷(理科)
一、选择题:本大题共10小题,每小题5分,共50分,每小题给出四个选项,只有一个选项符合题目要求.
1.(5分)若复数z满足2z+![]() =3﹣2i,其中i为虚数单位,则z=( )
=3﹣2i,其中i为虚数单位,则z=( )
A.1+2i B.1﹣2i C.﹣1+2i D.﹣1﹣2i
2.(5分)设集合A={y|y=2x,x∈R},B={x|x2﹣1<0},则A∪B=( )
A.(﹣1,1) B.(0,1) C.(﹣1,+∞) D.(0,+∞)
3.(5分)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
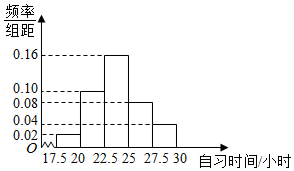
A.56 B.60 C.120 D.140
4.(5分)若变量x,y满足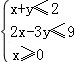 ,则x2+y2的最大值是( )
,则x2+y2的最大值是( )
A.4 B.9 C.10 D.12
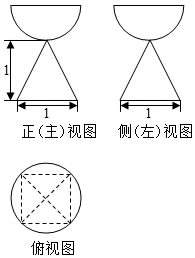
5.(5分)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )
A.![]() +
+![]() π B.
π B.![]() +
+![]() π C.
π C.![]() +
+![]() π D.1+
π D.1+![]() π
π
6.(5分)已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b相交”是“平面α和平面β相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.(5分)函数f(x)=(![]() sinx+cosx)(
sinx+cosx)(![]() cosx﹣sinx)的最小正周期是( )
cosx﹣sinx)的最小正周期是( )
A.![]() B.π C.
B.π C.![]() D.2π
D.2π
8.(5分)已知非零向量![]() ,
,![]() 满足4|
满足4|![]() |=3|
|=3|![]() |,cos<
|,cos<![]() ,
,![]() >=
>=![]() .若
.若![]() ⊥(t
⊥(t![]() +
+![]() ),则实数t的值为( )
),则实数t的值为( )
A.4 B.﹣4 C.![]() D.﹣
D.﹣![]()
9.(5分)已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x>![]() 时,f(x+
时,f(x+![]() )=f(x﹣
)=f(x﹣![]() ).则f(6)=( )
).则f(6)=( )
A.﹣2 B.1 C.0 D.2
10.(5分)若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )
A.y=sinx B.y=lnx C.y=ex D.y=x3
二、填空题:本大题共5小题,每小题5分,共25分.
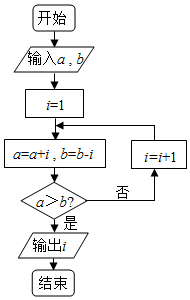
11.(5分)执行如图的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为 .
12.(5分)若(ax2+![]() )5的展开式中x5的系数是﹣80,则实数a=
.
)5的展开式中x5的系数是﹣80,则实数a=
.
13.(5分)已知双曲线E:![]() ﹣
﹣![]() =1(a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是
.
=1(a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是
.
14.(5分)在[﹣1,1]上随机地取一个数k,则事件“直线y=kx与圆(x﹣5)2+y2=9相交”发生的概率为 .
15.(5分)已知函数f(x)=![]() ,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是
.
,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是
.
三、解答题,:本大题共6小题,共75分.
16.(12分)在△ABC中,角A,B,C的对边分别为a,b,c,已知2(tanA+tanB)=![]() +
+![]() .
.
(Ⅰ)证明:a+b=2c;
(Ⅱ)求cosC的最小值.
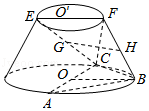
17.(12分)在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
(I)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB=![]() AC=2
AC=2![]() ,AB=BC,求二面角F﹣BC﹣A的余弦值.
,AB=BC,求二面角F﹣BC﹣A的余弦值.
18.(12分)已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)令cn=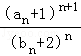 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
19.(12分)甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是![]() ,乙每轮猜对的概率是
,乙每轮猜对的概率是![]() ;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(I)“星队”至少猜对3个成语的概率;
(II)“星队”两轮得分之和为X的分布列和数学期望EX.
20.(13分)已知f(x)=a(x﹣lnx)+![]() ,a∈R.
,a∈R.
(I)讨论f(x)的单调性;
(II)当a=1时,证明f(x)>f′(x)+![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
21.(14分)平面直角坐标系xOy中,椭圆C:![]() +
+![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是![]() ,抛物线E:x2=2y的焦点F是C的一个顶点.
,抛物线E:x2=2y的焦点F是C的一个顶点.
(I)求椭圆C的方程;
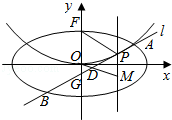
(Ⅱ)设P是E上的动点,且位于第一象限,E在点P处的切线l与C交于不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
(i)求证:点M在定直线上;
(ii)直线l与y轴交于点G,记△PFG的面积为S1,△PDM的面积为S2,求![]() 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标.
2016年山东省高考数学试卷(理科)
参考答案与试题解析
一、选择题:本大题共10小题,每小题5分,共50分,每小题给出四个选项,只有一个选项符合题目要求.
1.(5分)若复数z满足2z+![]() =3﹣2i,其中i为虚数单位,则z=( )
=3﹣2i,其中i为虚数单位,则z=( )
A.1+2i B.1﹣2i C.﹣1+2i D.﹣1﹣2i
【分析】设出复数z,通过复数方程求解即可.
【解答】解:复数z满足2z+![]() =3﹣2i,
=3﹣2i,
设z=a+bi,
可得:2a+2bi+a﹣bi=3﹣2i.
解得a=1,b=﹣2.
z=1﹣2i.
故选:B.
【点评】本题考查复数的代数形式混合运算,考查计算能力.
2.(5分)设集合A={y|y=2x,x∈R},B={x|x2﹣1<0},则A∪B=( )
A.(﹣1,1) B.(0,1) C.(﹣1,+∞) D.(0,+∞)
【分析】求解指数函数的值域化简A,求解一元二次不等式化简B,再由并集运算得答案.
【解答】解:∵A={y|y=2x,x∈R}=(0,+∞),
B={x|x2﹣1<0}=(﹣1,1),
∴A∪B=(0,+∞)∪(﹣1,1)=(﹣1,+∞).
故选:C.
【点评】本题考查并集及其运算,考查了指数函数的值域,考查一元二次不等式的解法,是基础题.
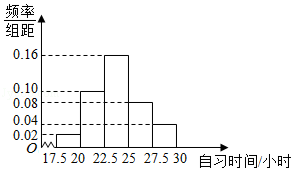
3.(5分)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60 C.120 D.140
【分析】根据已知中的频率分布直方图,先计算出自习时间不少于22.5小时的频率,进而可得自习时间不少于22.5小时的频数.
【解答】解:自习时间不少于22.5小时的频率为:(0.16+0.08+0.04)×2.5=0.7,
故自习时间不少于22.5小时的频率为:0.7×200=140,
故选:D.
【点评】本题考查的知识点是频率分布直方图,难度不大,属于基础题目.
4.(5分)若变量x,y满足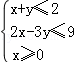 ,则x2+y2的最大值是( )
,则x2+y2的最大值是( )
A.4 B.9 C.10 D.12
【分析】由约束条件作出可行域,然后结合x2+y2的几何意义,即可行域内的动点与原点距离的平方求得x2+y2的最大值.
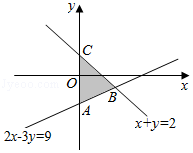
【解答】解:由约束条件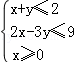 作出可行域如图,
作出可行域如图,
∵A(0,﹣3),C(0,2),
∴|OA|>|OC|,
联立![]() ,解得B(3,﹣1).
,解得B(3,﹣1).
∵![]() ,
,
∴x2+y2的最大值是10.
故选:C.
【点评】本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.
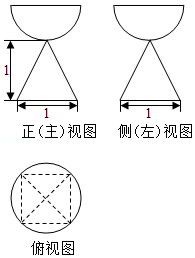
5.(5分)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )
A.![]() +
+![]() π B.
π B.![]() +
+![]() π C.
π C.![]() +
+![]() π D.1+
π D.1+![]() π
π
【分析】由已知中的三视图可得:该几何体上部是一个半球,下部是一个四棱锥,进而可得答案.
【解答】解:由已知中的三视图可得:该几何体上部是一个半球,下部是一个四棱锥,
半球的直径为棱锥的底面对角线,
由棱锥的底底面棱长为1,可得2R=![]() .
.
故R=![]() ,故半球的体积为:
,故半球的体积为:![]() =
=![]() π,
π,
棱锥的底面面积为:1,高为1,
故棱锥的体积V=![]() ,
,
故组合体的体积为:![]() +
+![]() π,
π,
故选:C.
【点评】本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.
6.(5分)已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b相交”是“平面α和平面β相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【分析】直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”⇒“平面α和平面β相交”,反之不成立.
【解答】解:直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”⇒“平面α和平面β相交”,
反之不成立.
∴“直线a和直线b相交”是“平面α和平面β相交”的充分不必要条件.
故选:A.
【点评】本题考查了空间位置关系、简易逻辑的判定方法,考查了推理能力,属于基础题.
7.(5分)函数f(x)=(![]() sinx+cosx)(
sinx+cosx)(![]() cosx﹣sinx)的最小正周期是( )
cosx﹣sinx)的最小正周期是( )
A.![]() B.π C.
B.π C.![]() D.2π
D.2π
【分析】利用和差角及二倍角公式,化简函数的解析式,进而可得函数的周期.
【解答】解:函数f(x)=(![]() sinx+cosx)(
sinx+cosx)(![]() cosx﹣sinx)=2sin(x+
cosx﹣sinx)=2sin(x+![]() )•2cos(x+
)•2cos(x+![]() )=2sin(2x+
)=2sin(2x+![]() ),
),
∴T=π,
故选:B.
【点评】本题考查的知识点是和差角及二倍角公式,三角函数的周期,难度中档.
8.(5分)已知非零向量![]() ,
,![]() 满足4|
满足4|![]() |=3|
|=3|![]() |,cos<
|,cos<![]() ,
,![]() >=
>=![]() .若
.若![]() ⊥(t
⊥(t![]() +
+![]() ),则实数t的值为( )
),则实数t的值为( )
A.4 B.﹣4 C.![]() D.﹣
D.﹣![]()
【分析】若![]() ⊥(t
⊥(t![]() +
+![]() ),则
),则![]() •(t
•(t![]() +
+![]() )=0,进而可得实数t的值.
)=0,进而可得实数t的值.
【解答】解:∵4|![]() |=3|
|=3|![]() |,cos<
|,cos<![]() ,
,![]() >=
>=![]() ,
,![]() ⊥(t
⊥(t![]() +
+![]() ),
),
∴![]() •(t
•(t![]() +
+![]() )=t
)=t![]() •
•![]() +
+![]() 2=t|
2=t|![]() |•|
|•|![]() |•
|•![]() +|
+|![]() |2=(
|2=(![]() )|
)|![]() |2=0,
|2=0,
解得:t=﹣4,
故选:B.
【点评】本题考查的知识点是平面向量数量积的运算,向量垂直的充要条件,难度不大,属于基础题.
9.(5分)已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x>![]() 时,f(x+
时,f(x+![]() )=f(x﹣
)=f(x﹣![]() ).则f(6)=( )
).则f(6)=( )
A.﹣2 B.1 C.0 D.2
【分析】求得函数的周期为1,再利用当﹣1≤x≤1时,f(﹣x)=﹣f(x),得到f(1)=﹣f(﹣1),当x<0时,f(x)=x3﹣1,得到f(﹣1)=﹣2,即可得出结论.
【解答】解:∵当x>![]() 时,f(x+
时,f(x+![]() )=f(x﹣
)=f(x﹣![]() ),
),
∴当x>![]() 时,f(x+1)=f(x),即周期为1.
时,f(x+1)=f(x),即周期为1.
∴f(6)=f(1),
∵当﹣1≤x≤1时,f(﹣x)=﹣f(x),
∴f(1)=﹣f(﹣1),
∵当x<0时,f(x)=x3﹣1,
∴f(﹣1)=﹣2,
∴f(1)=﹣f(﹣1)=2,
∴f(6)=2.
故选:D.
【点评】本题考查函数值的计算,考查函数的周期性,考查学生的计算能力,属于中档题.
10.(5分)若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )
A.y=sinx B.y=lnx C.y=ex D.y=x3
【分析】若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则函数y=f(x)的导函数上存在两点,使这点的导函数值乘积为﹣1,进而可得答案.
【解答】解:函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,
则函数y=f(x)的导函数上存在两点,使这点的导函数值乘积为﹣1,
当y=sinx时,y′=cosx,满足条件;
当y=lnx时,y′=![]() >0恒成立,不满足条件;
>0恒成立,不满足条件;
当y=ex时,y′=ex>0恒成立,不满足条件;
当y=x3时,y′=3x2>0恒成立,不满足条件;
故选:A.
【点评】本题考查的知识点是利用导数研究曲线上某点切线方程,转化思想,难度中档.
二、填空题:本大题共5小题,每小题5分,共25分.
11.(5分)执行如图的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为 3 .

【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量i的值,模拟程序的运行过程,可得答案.
【解答】解:∵输入的a,b的值分别为0和9,i=1.
第一次执行循环体后:a=1,b=8,不满足条件a>b,故i=2;
第二次执行循环体后:a=3,b=6,不满足条件a>b,故i=3;
第三次执行循环体后:a=6,b=3,满足条件a>b,
故输出的i值为:3,
故答案为:3
【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程序法进行解答.
12.(5分)若(ax2+![]() )5的展开式中x5的系数是﹣80,则实数a= ﹣2 .
)5的展开式中x5的系数是﹣80,则实数a= ﹣2 .
【分析】利用二项展开式的通项公式Tr+1=![]() (ax2)5﹣r
(ax2)5﹣r![]() ,化简可得求的x5的系数.
,化简可得求的x5的系数.
【解答】解:(ax2+![]() )5的展开式的通项公式Tr+1=
)5的展开式的通项公式Tr+1=![]() (ax2)5﹣r
(ax2)5﹣r![]() =
=![]() a5﹣r
a5﹣r![]() ,
,
令10﹣![]() =5,解得r=2.
=5,解得r=2.
∵(ax2+![]() )5的展开式中x5的系数是﹣80
)5的展开式中x5的系数是﹣80
∴![]() a3=﹣80,
a3=﹣80,
得a=﹣2.
【点评】考查了利用二项式定理的性质求二项式展开式的系数,属常规题型.
13.(5分)已知双曲线E:![]() ﹣
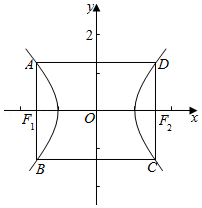
﹣![]() =1(a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是 2 .
=1(a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是 2 .
【分析】可令x=c,代入双曲线的方程,求得y=±![]() ,再由题意设出A,B,C,D的坐标,由2|AB|=3|BC|,可得a,b,c的方程,运用离心率公式计算即可得到所求值.
,再由题意设出A,B,C,D的坐标,由2|AB|=3|BC|,可得a,b,c的方程,运用离心率公式计算即可得到所求值.
【解答】解:令x=c,代入双曲线的方程可得y=±b![]() =±
=±![]() ,
,
由题意可设A(﹣c,![]() ),B(﹣c,﹣
),B(﹣c,﹣![]() ),C(c,﹣
),C(c,﹣![]() ),D(c,
),D(c,![]() ),
),
由2|AB|=3|BC|,可得
2•![]() =3•2c,即为2b2=3ac,
=3•2c,即为2b2=3ac,
由b2=c2﹣a2,e=![]() ,可得2e2﹣3e﹣2=0,
,可得2e2﹣3e﹣2=0,
解得e=2(负的舍去).
故答案为:2.
【点评】本题考查双曲线的离心率的求法,注意运用方程的思想,正确设出A,B,C,D的坐标是解题的关键,考查运算能力,属于中档题.
14.(5分)在[﹣1,1]上随机地取一个数k,则事件“直线y=kx与圆(x﹣5)2+y2=9相交”发生的概率为 ![]() .
.
【分析】利用圆心到直线的距离小于半径可得到直线与圆相交,可求出满足条件的k,最后根据几何概型的概率公式可求出所求.
【解答】解:圆(x﹣5)2+y2=9的圆心为(5,0),半径为3.
圆心到直线y=kx的距离为![]() ,
,
要使直线y=kx与圆(x﹣5)2+y2=9相交,则![]() <3,解得﹣
<3,解得﹣![]() <k<
<k<![]() .
.
∴在区间[﹣1,1]上随机取一个数k,使直线y=kx与圆(x﹣5)2+y2=9相交相交的概率为![]() =
=![]() .
.
故答案为:![]() .
.
【点评】本题主要考查了几何概型的概率,以及直线与圆相交的性质,解题的关键弄清概率类型,同时考查了计算能力,属于基础题.
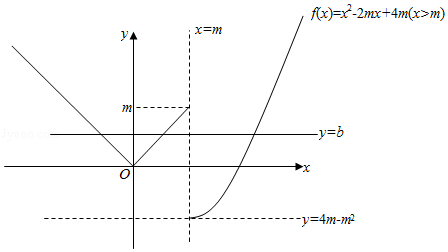
15.(5分)已知函数f(x)=![]() ,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 (3,+∞) .
,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 (3,+∞) .
【分析】作出函数f(x)=![]() 的图象,依题意,可得4m﹣m2<m(m>0),解之即可.
的图象,依题意,可得4m﹣m2<m(m>0),解之即可.
【解答】解:当m>0时,函数f(x)=![]() 的图象如下:
的图象如下:
∵x>m时,f(x)=x2﹣2mx+4m=(x﹣m)2+4m﹣m2>4m﹣m2,
∴y要使得关于x的方程f(x)=b有三个不同的根,
必须4m﹣m2<m(m>0),
即m2>3m(m>0),
解得m>3,
∴m的取值范围是(3,+∞),
故答案为:(3,+∞).
【点评】本题考查根的存在性及根的个数判断,数形结合思想的运用是关键,分析得到4m﹣m2<m是难点,属于中档题.
三、解答题,:本大题共6小题,共75分.
16.(12分)在△ABC中,角A,B,C的对边分别为a,b,c,已知2(tanA+tanB)=![]() +
+![]() .
.
(Ⅰ)证明:a+b=2c;
(Ⅱ)求cosC的最小值.
【分析】(Ⅰ)由切化弦公式![]() ,带入
,带入![]() 并整理可得2(sinAcosB+cosAsinB)=sinA+cosB,这样根据两角和的正弦公式即可得到sinA+sinB=2sinC,从而根据正弦定理便可得出a+b=2c;
并整理可得2(sinAcosB+cosAsinB)=sinA+cosB,这样根据两角和的正弦公式即可得到sinA+sinB=2sinC,从而根据正弦定理便可得出a+b=2c;
(Ⅱ)根据a+b=2c,两边平方便可得出a2+b2+2ab=4c2,从而得出a2+b2=4c2﹣2ab,并由不等式a2+b2≥2ab得出c2≥ab,也就得到了![]() ,这样由余弦定理便可得出
,这样由余弦定理便可得出![]() ,从而得出cosC的范围,进而便可得出cosC的最小值.
,从而得出cosC的范围,进而便可得出cosC的最小值.
【解答】解:(Ⅰ)证明:由![]() 得:
得:
![]() ;
;
∴两边同乘以cosAcosB得,2(sinAcosB+cosAsinB)=sinA+sinB;
∴2sin(A+B)=sinA+sinB;
即sinA+sinB=2sinC(1);
根据正弦定理,![]() ;
;
∴![]() ,带入(1)得:
,带入(1)得:![]() ;
;
∴a+b=2c;
(Ⅱ)a+b=2c;
∴(a+b)2=a2+b2+2ab=4c2;
∴a2+b2=4c2﹣2ab,且4c2≥4ab,当且仅当a=b时取等号;
又a,b>0;
∴![]() ;
;
∴由余弦定理,![]() =
=![]()
![]() ;
;
∴cosC的最小值为![]() .
.
【点评】考查切化弦公式,两角和的正弦公式,三角形的内角和为π,以及三角函数的诱导公式,正余弦定理,不等式a2+b2≥2ab的应用,不等式的性质.
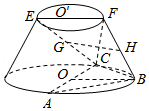
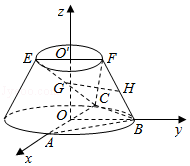
17.(12分)在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
(I)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB=![]() AC=2
AC=2![]() ,AB=BC,求二面角F﹣BC﹣A的余弦值.
,AB=BC,求二面角F﹣BC﹣A的余弦值.
【分析】(Ⅰ)取FC中点Q,连结GQ、QH,推导出平面GQH∥平面ABC,由此能证明GH∥平面ABC.
(Ⅱ)由AB=BC,知BO⊥AC,以O为原点,OA为x轴,OB为y轴,OO′为z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣BC﹣A的余弦值.
【解答】证明:(Ⅰ)取FC中点Q,连结GQ、QH,
∵G、H为EC、FB的中点,
∴GQ![]()
![]() ,QH
,QH![]()
![]() ,
,
又∵EF∥BO,∴GQ∥BO,
∵QH∩GQ=Q,BC∩BO=B,
∴平面GQH∥平面ABC,
∵GH⊂面GQH,∴GH∥平面ABC.
解:(Ⅱ)∵AB=BC,∴BO⊥AC,
又∵OO′⊥面ABC,
∴以O为原点,OA为x轴,OB为y轴,OO′为z轴,建立空间直角坐标系,
则A(![]() ,0,0),C(﹣2
,0,0),C(﹣2![]() ,0,0),B(0,2
,0,0),B(0,2![]() ,0),O′(0,0,3),F(0,
,0),O′(0,0,3),F(0,![]() ,3),
,3),
![]() =(﹣2
=(﹣2![]() ,﹣
,﹣![]() ,﹣3),
,﹣3),![]() =(2
=(2![]() ,2
,2![]() ,0),
,0),
由题意可知面ABC的法向量为![]() =(0,0,3),
=(0,0,3),
设![]() =(x0,y0,z0)为面FCB的法向量,
=(x0,y0,z0)为面FCB的法向量,
则![]() ,即
,即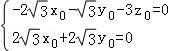 ,
,
取x0=1,则![]() =(1,﹣1,﹣
=(1,﹣1,﹣![]() ),
),
∴cos<![]() ,
,![]() >=
>=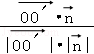 =﹣
=﹣![]() .
.
∵二面角F﹣BC﹣A的平面角是锐角,
∴二面角F﹣BC﹣A的余弦值为![]() .
.
【点评】本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.
18.(12分)已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)令cn= ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
【分析】(Ⅰ)求出数列{an}的通项公式,再求数列{bn}的通项公式;
(Ⅱ)求出数列{cn}的通项,利用错位相减法求数列{cn}的前n项和Tn.
【解答】解:(Ⅰ)Sn=3n2+8n,
∴n≥2时,an=Sn﹣Sn﹣1=6n+5,
n=1时,a1=S1=11,∴an=6n+5;
∵an=bn+bn+1,
∴an﹣1=bn﹣1+bn,
∴an﹣an﹣1=bn+1﹣bn﹣1.
∴2d=6,
∴d=3,
∵a1=b1+b2,
∴11=2b1+3,
∴b1=4,
∴bn=4+3(n﹣1)=3n+1;
(Ⅱ)cn= =
=![]() =
=![]() =
=![]() =
=![]() =
=![]() =
=![]() =6(n+1)•2n,
=6(n+1)•2n,
∴Tn=6[2•2+3•22+…+(n+1)•2n]①,
∴2Tn=6[2•22+3•23+…+n•2n+(n+1)•2n+1]②,
①﹣②可得
﹣Tn=6[2•2+22+23+…+2n﹣(n+1)•2n+1]
=12+6×![]() ﹣6(n+1)•2n+1
﹣6(n+1)•2n+1
=(﹣6n)•2n+1=﹣3n•2n+2,
∴Tn=3n•2n+2.
【点评】本题考查数列的通项与求和,着重考查等差数列的通项与错位相减法的运用,考查分析与运算能力,属于中档题.
19.(12分)甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是![]() ,乙每轮猜对的概率是
,乙每轮猜对的概率是![]() ;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(I)“星队”至少猜对3个成语的概率;
(II)“星队”两轮得分之和为X的分布列和数学期望EX.
【分析】(I)“星队”至少猜对3个成语包含“甲猜对1个,乙猜对2个”,“甲猜对2个,乙猜对1个”,“甲猜对2个,乙猜对2个”三个基本事件,进而可得答案;
(II)由已知可得:“星队”两轮得分之和为X可能为:0,1,2,3,4,6,进而得到X的分布列和数学期望.
【解答】解:(I)“星队”至少猜对3个成语包含“甲猜对1个,乙猜对2个”,“甲猜对2个,乙猜对1个”,“甲猜对2个,乙猜对2个”三个基本事件,
故概率P=![]() +
+ +
+![]() =
=![]() +
+![]() +
+![]() =
=![]() ,
,
(II)“星队”两轮得分之和为X可能为:0,1,2,3,4,6,
则P(X=0)=![]() =
=![]() ,
,
P(X=1)=2×[![]() +
+![]() ]=
]=![]() ,
,
P(X=2)=![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
,
P(X=3)=2×![]() =
=![]() ,
,
P(X=4)=2×[![]() +
+![]() ]=
]=![]()
P(X=6)=![]() =
=![]()
故X的分布列如下图所示:
X |
0 |
1 |
2 |
3 |
4 |
6 |
P |
|
|
|
|
|
|
∴数学期望EX=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() +4×
+4×![]() +6×
+6×![]() =
=![]() =
=![]()
【点评】本题考查离散型随机变量的分布列和数学期望,属中档题.
20.(13分)已知f(x)=a(x﹣lnx)+![]() ,a∈R.
,a∈R.
(I)讨论f(x)的单调性;
(II)当a=1时,证明f(x)>f′(x)+![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
【分析】(Ⅰ)求出原函数的导函数,然后对a分类分析导函数的符号,由导函数的符号确定原函数的单调性;
(Ⅱ)构造函数F(x)=f(x)﹣f′(x),令g(x)=x﹣lnx,h(x)=![]()
![]() .则F(x)=f(x)﹣f′(x)=g(x)+h(x),利用导数分别求g(x)与h(x)的最小值得到F(x)>
.则F(x)=f(x)﹣f′(x)=g(x)+h(x),利用导数分别求g(x)与h(x)的最小值得到F(x)>![]() 恒成立.由此可得f(x)>f′(x)+
恒成立.由此可得f(x)>f′(x)+![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
【解答】(Ⅰ)解:由f(x)=a(x﹣lnx)+![]() ,
,
得f′(x)=a(1﹣![]() )+
)+![]()
=![]() =
=![]() (x>0).
(x>0).
若a≤0,则ax2﹣2<0恒成立,
∴当x∈(0,1)时,f′(x)>0,f(x)为增函数,
当x∈(1,+∞)时,f′(x)<0,f(x)为减函数;
当a>0,若0<a<2,当x∈(0,1)和(![]() ,+∞)时,f′(x)>0,f(x)为增函数,
,+∞)时,f′(x)>0,f(x)为增函数,
当x∈(1,![]() )时,f′(x)<0,f(x)为减函数;
)时,f′(x)<0,f(x)为减函数;
若a=2,f′(x)≥0恒成立,f(x)在(0,+∞)上为增函数;
若a>2,当x∈(0,![]() )和(1,+∞)时,f′(x)>0,f(x)为增函数,
)和(1,+∞)时,f′(x)>0,f(x)为增函数,
当x∈(![]() ,1)时,f′(x)<0,f(x)为减函数;
,1)时,f′(x)<0,f(x)为减函数;
(Ⅱ)解:∵a=1,
令F(x)=f(x)﹣f′(x)=x﹣lnx![]()
![]() ﹣1
﹣1![]() =x﹣lnx+
=x﹣lnx+![]()
![]() .
.
令g(x)=x﹣lnx,h(x)=![]()
![]() .
.
则F(x)=f(x)﹣f′(x)=g(x)+h(x),
由![]() ,可得g(x)≥g(1)=1,当且仅当x=1时取等号;
,可得g(x)≥g(1)=1,当且仅当x=1时取等号;
又![]() ,
,
设φ(x)=﹣3x2﹣2x+6,则φ(x)在[1,2]上单调递减,
且φ(1)=1,φ(2)=﹣10,
∴在[1,2]上存在x0,使得x∈(1,x0) 时φ(x0)>0,x∈(x0,2)时,φ(x0)<0,
∴函数h(x)在(1,x0)上单调递增;在(x0,2)上单调递减,
由于h(1)=1,h(2)=![]() ,因此h(x)≥h(2)=
,因此h(x)≥h(2)=![]() ,当且仅当x=2取等号,
,当且仅当x=2取等号,
∴f(x)﹣f′(x)=g(x)+h(x)>g(1)+h(2)=![]() ,
,
∴F(x)>![]() 恒成立.
恒成立.
即f(x)>f′(x)+![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
【点评】本题考查利用导数加以函数的单调性,考查了利用导数求函数的最值,考查了分类讨论的数学思想方法和数学转化思想方法,是压轴题.
21.(14分)平面直角坐标系xOy中,椭圆C:![]() +
+![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是![]() ,抛物线E:x2=2y的焦点F是C的一个顶点.
,抛物线E:x2=2y的焦点F是C的一个顶点.
(I)求椭圆C的方程;
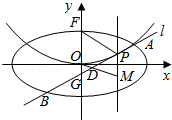
(Ⅱ)设P是E上的动点,且位于第一象限,E在点P处的切线l与C交于不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
(i)求证:点M在定直线上;
(ii)直线l与y轴交于点G,记△PFG的面积为S1,△PDM的面积为S2,求![]() 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标.
【分析】(I)运用椭圆的离心率公式和抛物线的焦点坐标,以及椭圆的a,b,c的关系,解得a,b,进而得到椭圆的方程;
(Ⅱ)(i)设P(x0,y0),运用导数求得切线的斜率和方程,代入椭圆方程,运用韦达定理,可得中点D的坐标,求得OD的方程,再令x=x0,可得y=﹣![]() .进而得到定直线;
.进而得到定直线;
(ii)由直线l的方程为y=x0x﹣y0,令x=0,可得G(0,﹣y0),运用三角形的面积公式,可得S1=![]() |FG|•|x0|=
|FG|•|x0|=![]() x0•(
x0•(![]() +y0),S2=
+y0),S2=![]() |PM|•|x0﹣
|PM|•|x0﹣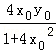 |,化简整理,再1+2x02=t(t≥1),整理可得t的二次方程,进而得到最大值及此时P的坐标.
|,化简整理,再1+2x02=t(t≥1),整理可得t的二次方程,进而得到最大值及此时P的坐标.
【解答】解:(I)由题意可得e=![]() =
=![]() ,抛物线E:x2=2y的焦点F为(0,
,抛物线E:x2=2y的焦点F为(0,![]() ),
),
即有b=![]() ,a2﹣c2=
,a2﹣c2=![]() ,
,
解得a=1,c=![]() ,
,
可得椭圆的方程为x2+4y2=1;
(Ⅱ)(i)证明:设P(x0,y0),可得x02=2y0,
由y=![]() x2的导数为y′=x,即有切线的斜率为x0,
x2的导数为y′=x,即有切线的斜率为x0,
则切线的方程为y﹣y0=x0(x﹣x0),
可化为y=x0x﹣y0,代入椭圆方程,
可得(1+4x02)x2﹣8x0y0x+4y02﹣1=0,
△=64x02y02﹣4(1+4x02)(4y02﹣1)>0,可得1+4x02>4y02.
设A(x1,y1),B(x2,y2),
可得x1+x2=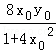 ,即有中点D(
,即有中点D(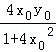 ,﹣
,﹣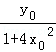 ),
),
直线OD的方程为y=﹣![]() x,可令x=x0,可得y=﹣
x,可令x=x0,可得y=﹣![]() .
.
即有点M在定直线y=﹣![]() 上;
上;
(ii)直线l的方程为y=x0x﹣y0,令x=0,可得G(0,﹣y0),
则S1=![]() |FG|•|x0|=
|FG|•|x0|=![]() x0•(
x0•(![]() +y0)=
+y0)=![]() x0(1+x02);
x0(1+x02);
S2=![]() |PM|•|x0﹣
|PM|•|x0﹣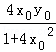 |=
|=![]() (y0+
(y0+![]() )•
)•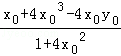 =
=![]() x0•
x0•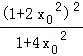 ,
,
则![]() =
=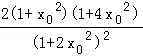 ,
,
令1+2x02=t(t≥1),则![]() =
=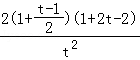 =
=![]()
=![]() =2+
=2+![]() ﹣
﹣![]() =﹣(
=﹣(![]() ﹣
﹣![]() )2+
)2+![]() ,
,
则当t=2,即x0=![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
此时点P的坐标为(![]() ,
,![]() ).
).
【点评】本题考查椭圆的方程的求法,注意运用椭圆的离心率和抛物线的焦点坐标,考查直线和抛物线斜的条件,以及直线方程的运用,考查三角形的面积的计算,以及化简整理的运算能力,属于难题.
第