11.2.1三角形的内角和
基础知识
选择题
1.下列说法正确的是( )
A.三角形的内角中最多有一个锐角; B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角; D.三角形的内角都大于60°
答案:C
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2.(2012
广东省梅州市)
如图,在折纸活动中,小明制作了一张纸片,点、分别是边、上,将沿着折叠压平,与重合,若,则( )
2.(2012
广东省梅州市)
如图,在折纸活动中,小明制作了一张纸片,点、分别是边、上,将沿着折叠压平,与重合,若,则( )
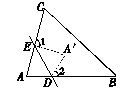
![]()
![]()
![]()
![]() (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
答案:A
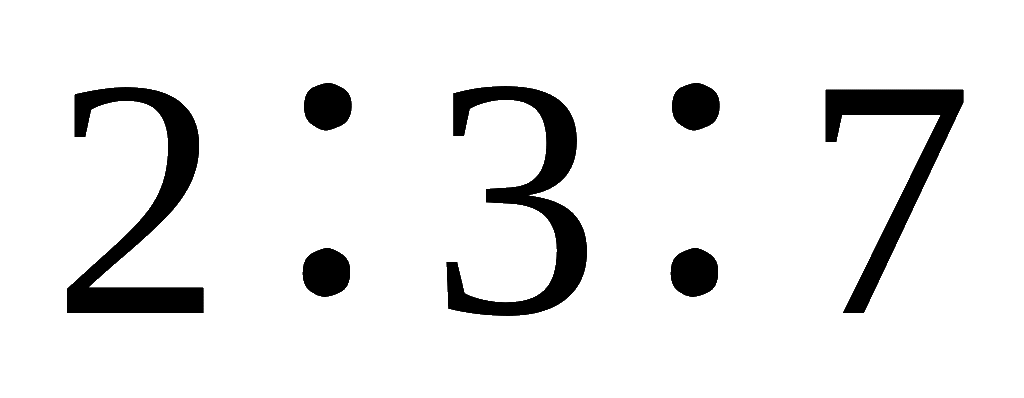 3.
(2012 山东省滨州市)
一个三角形的三个内角的度数之比为,则这个三角形一定是( )
3.
(2012 山东省滨州市)
一个三角形的三个内角的度数之比为,则这个三角形一定是( )
(A)等腰三角形 (B)直角三角形 (C)锐角三角形 (D)钝角三角形
答案:D
![]()
![]()
![]()
![]()
![]() 4.
(2012 云南省昆明市)
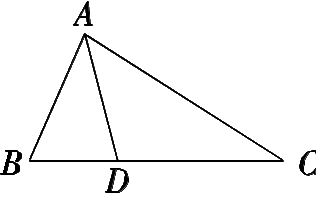
如图,在中,,是的角平分线,则的度数为( ).
4.
(2012 云南省昆明市)
如图,在中,,是的角平分线,则的度数为( ).
![]()
![]()
![]()
![]() (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
答案:A
![]() 5.
(2012 福建省漳州市)
将一副直角三角板,按如图所示叠放在一起,则图中∠的度数是( )
5.
(2012 福建省漳州市)
将一副直角三角板,按如图所示叠放在一起,则图中∠的度数是( )
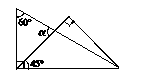
(A)45o (B)60o (C)75o (D)90o
答案:C
6. (2012 四川省绵阳市) 如图,将等腰直角三角形沿虚线裁去顶角后,∠1 +∠2 =( ).
A.225° B.235° C.270° D.与虚线的位置有关
![]()
答案:C
7. (2012 广西来宾市) 如图,在△ABC中,已知∠A=80°,∠B=60°,DE∥BC,那么∠CED的大小是 ( )
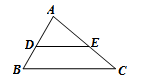
A.40° B.60° C.120° D.140°
答案:D
![]() 8.
(2012 山东省聊城市)
将一副三角板按如图所示摆放,图中的度数是(
)
8.
(2012 山东省聊城市)
将一副三角板按如图所示摆放,图中的度数是(
)
![]()
![]()
![]()
![]() (A) (B) (C) (D)
(A) (B) (C) (D)
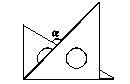
答案:C
9.如图,ABCDE是封闭折线,则∠A+∠B+∠C+∠D+∠E为( )度.
A.180 B.270 C.360 D.540
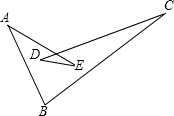
答案:A
10.直角三角形两锐角的平分线所夹的钝角等于( )
A.100° B.120° C.135° D.150°
答案:C
11.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
A.40°B.30°C.20°D.10°
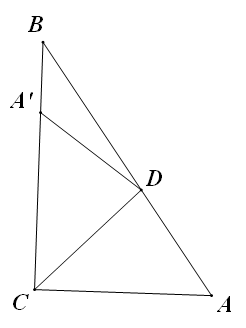
答案:D
12.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A-∠B=∠C B.∠A=3∠C,∠B=2∠C
![]() C.∠A=∠B=2∠C D.∠A=∠B=∠C
C.∠A=∠B=2∠C D.∠A=∠B=∠C
答案:C
13.如图,在三角形ABC中,已知∠ABC=70º,∠ACB=60º,BE⊥AC于E,CF⊥AB于F,H是BE和CF的交点,则∠EHF=( )
100º B. 110º C. 120º D.130º

答案:D
14.如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图
中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )
A.180° B.270° C.360° D.无法确定
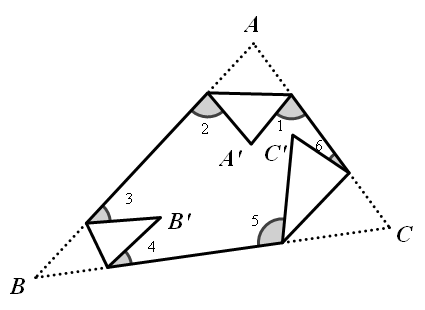
答案:C
填空题
三角形中,若最大内角等于最小内角的2倍,最大内角又比另一个内角大20°,则此三角形的最小内角的度数是________.
答案:40°
2.在△ABC中,若∠A+∠B=∠C,则此三角形为_______三角形;若∠A+∠B<∠C,则此三角形是_____三角形.
答案:直角;钝角
3.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A=_______度.
答案:84°
4.如图所示,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为________.
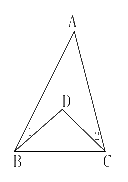
答案:80°
5.(2013•上海)当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为 .
答案:30º
![]()
![]()
![]()
![]()
![]()
![]() 6.
(2012 内蒙古呼和浩特市)
如图,在中,,三角形的外角和的平分线交于点,则=____________.
6.
(2012 内蒙古呼和浩特市)
如图,在中,,三角形的外角和的平分线交于点,则=____________.
答案:66.5°
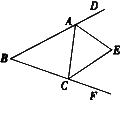
7. (2012 江苏省徐州市) 将一副直角三角板如图放置.若AE∥BC,则∠AFD= °.
答案:75°
8.如图,AB∥CD,∠A=32°,∠AEB=100°,则∠C的度数是 度.
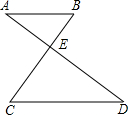
答案:48º
9.△ABC中,∠A=∠B+∠C,则∠A= 度.
答案:90
![]()
![]() 10.在△ABC中,已知∠A=∠B=∠C,则三角形的形状是
三角形.
10.在△ABC中,已知∠A=∠B=∠C,则三角形的形状是
三角形.
答案:直角三角形
11.已知△ABC中,∠A=2(∠B+∠C),则∠A的度数为 度.
答案:120
8.如图,在△ABC中,∠1=∠2,∠3=∠4,∠BOC=120°,则∠A= .

答案:60º
12.如图,AD、AE分别是△ABC的高和角平分线,∠B=58°,∠C=36°,∠EAD=
.

答案:11º
13.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=150°,
则∠EDF=________度.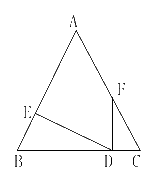
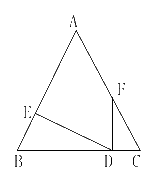
答案:60°
14.如图,∠A+∠B+∠C+∠D+∠E+∠F= .
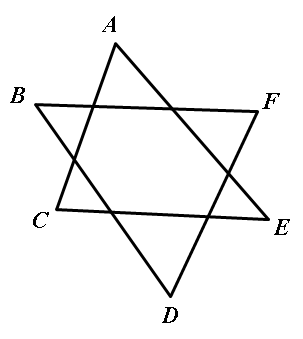
答案:360°
解答题
1.在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.
设∠A=x°,则∠B=(x+5)°, ∠C=(x+25)°可列方程
X+x+5+x+25=180
解得:x=50°
所以∠A=50°,∠B=55°, ∠C=75°
2.已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P.求证:∠P=90°.
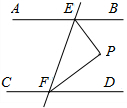
![]()
![]()
![]() 证明:∵AB∥CD,
证明:∵AB∥CD,
∴∠BEF+∠DFE=180°.
又∵∠BEF的平分线与∠DFE的平分线相交于点P,
∴∠PEF=∠BEF,∠PFE=∠DFE,
∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°.
∵∠PEF+∠PFE+∠P=180°,
∴∠P=90°.
3.如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠A=40°,∠B=72°.
(1)求∠DCE的度数;
(2)试写出∠DCE与∠A、∠B的之间的关系式.(不必证明)
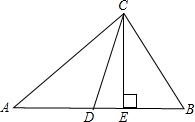
答案:(1)在⊿ABC中,∠ACB=180º-∠A-∠B=68º,
∵CD是∠ACB的角平分线
![]() ∴∠BCD=∠ACB=34º
∴∠BCD=∠ACB=34º
∵CE⊥AB,∠B=72º
∴∠BCE=18º
∴∠DCE=∠BCD-∠BCE=34º-18º=16º.
![]() (2)∠DCE=(∠B-∠A).
(2)∠DCE=(∠B-∠A).
4.如图,已知在三角形ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
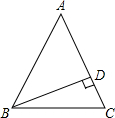
解:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°-∠C=18°.
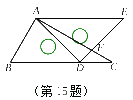
5.如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=40°,求∠XBA+∠XCA的度数.
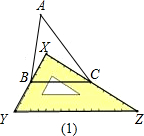
解:∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°,
∵∠X=90°,
∴∠XBC+∠XCB=180°-90°=90°,
∴∠XBA+∠XCA=(∠ABC+∠ACB)-(∠XBC+∠XCB)=140°-90°=50°.
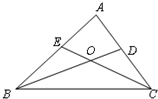
6.如图,△ABC中,∠ABC、∠ACB的平分线相交于点O.
(1)若∠ABC=45°,∠ACB=55°,则∠BOC
的度数是
;
(2)若∠A=80°,求∠BOC
的度数;
(3)若∠A=α,∠BOC=β,请猜想α与β之间的数量关系,并说明理由.
![]()
![]()
![]()
![]() 解:(1)∵∠ABC和∠ACB的平分线BD,CE相交于点O,
解:(1)∵∠ABC和∠ACB的平分线BD,CE相交于点O,
∴∠DBC=∠ABC,∠ECB=∠ACB,又∠ABC=45°,∠ACB=55°,
∴∠DBC=22.5°,∠ECB=27.5°,
∴∠BOC=180°-∠DBC-∠ECB=180°-22.5°-27.5°=130°,
故答案为:130°;
(2)∵∠A=80°,
∴∠ABC+∠ACB=180°-80°=100°,
又∠ABC和∠ACB的平分线BD,CE相交于点O,
∴∠DBC=∠ABC,∠ECB=∠ACB,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∴∠DBC+∠ECB=(∠ABC+∠ACB)=50°,
∴∠DBC+∠ECB=(∠ABC+∠ACB)=50°,
则∠BOC=180°-(∠DBC+∠ECB)=180°-50°=130°;
(3)β=90+α,
理由如下:∵∠ABC、∠ACB的平分线相交于点O,
∴∠OBC=∠ABC、∠0CB=∠ACB,
∴∠OBC+∠0CB=
∠ABC+∠ACB=(180°-α)=90°-α,
∴β=180°-(∠OBC+∠0CB)=180°-(90°-α)=90°+α.
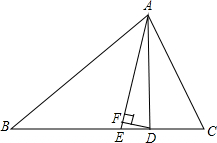
如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE于F,求∠ADF的度数.
![]() 解:∵∠B=40°,∠C=60°,
解:∵∠B=40°,∠C=60°,
∴∠BAC=80°.
∵AE平分∠BAC交BC于E,
∴∠BAE=∠BAC=40°,
∴∠AED=∠B+∠BAE=80°.
∵AD⊥BC,
∴∠DAE=90°-80°=10°
∵DF⊥AE,
∴∠ADF=90°-10°=80.
能力提升
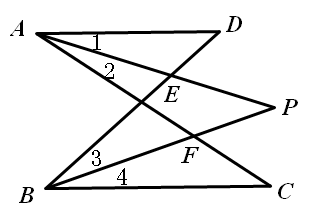
1.如图,已知:∠1= ∠2, ∠3= ∠4, ∠C=32°, ∠D=28°,求∠P的度数。
答案:
∵∠AED=∠BEP
∴∠1+∠D=∠3+∠P
∴∠D-∠P=∠3-∠1
∵∠AFP=∠BFC
∴∠2+∠P=∠4+∠C
∴∠P-∠C=∠4-∠2
∵∠1=∠2, ∠3=∠4
∴∠D-∠P=∠P-∠C
![]() ∴∠P=(∠C+∠D)=30º
∴∠P=(∠C+∠D)=30º
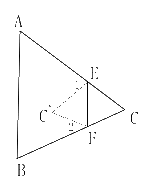
2.如图所示,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.
解:∵∠1=180°-2∠CEF,∠2=180°-2∠CFE,
∴∠1+∠2=360°-2(∠CEF+ ∠CFE)
=360°-2(180°-∠C)
=360°-360°+2∠C=2∠C.
将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C.
(1)如图1,当∠A=45°时,∠ABC+∠ACB=
度,∠DBC+∠DCB=
度;
(2)如图2,改变直角三角板DEF的位置,使该三角板的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD的大小是否发生变化?若变化,请举例说明;若没有变化,请探究∠ABD+∠ACD与∠A的关系.
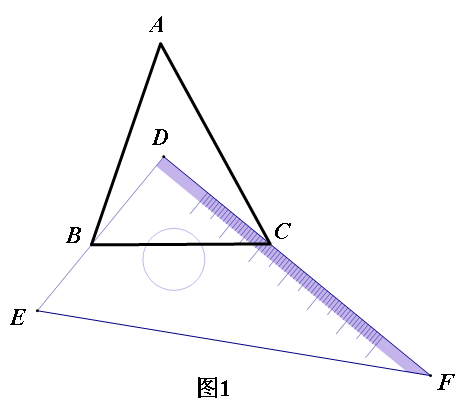
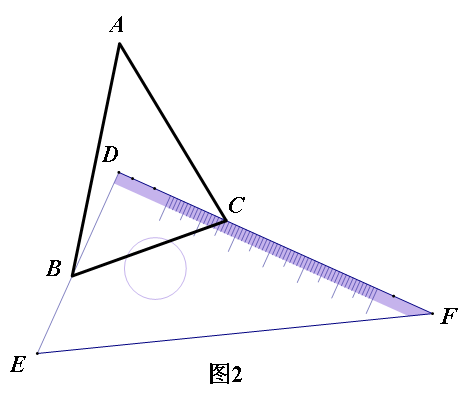
解:(1)在△ABC中,∵∠A=45°,
∴∠ABC+∠ACB=180°-45°=135°,
在△DBC中,∵∠DBC=90°,
∴∠DBC+∠DCB=180°-90°=90°;
故答案135,90.
(2)不变.理由如下:
∵90°+(∠ABD+∠ACD)+∠A=180°,
∴(∠ABD+∠ACD)+∠A=90°,
∴∠ABD+∠ACD=90°-∠A.