第8章 二元一次方程组 期末考题好题精选训练

一、选择题

1．（2016年•滕州市期末）早餐店里，李明妈妈买了5个馒头，3个包子，老板少要1元，只要10元；王红爸爸买了8个馒头，6个包子，老板九折优惠，只要18元．若馒头每个x元，包子每个y元，则所列二元一次方程组正确的是（　　）

A． B．

C． D．

2．（2016年•安岳县期末）已知是方程组的解，则a+b+c的值是（　　）

A．3 B．2 C．1 D．无法确定

3．（河北省中考）根据图中提供的信息，可知一个杯子的价格是（　　）

A．51元 B．35元 C．8元 D．7.5元

4．（2014•烟台）按如图的运算程序，能使输出结果为3的x，y的值是（　　）

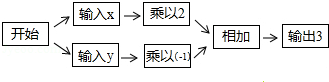
A．x=5，y=﹣2 B．x=3，y=﹣3 C．x=﹣4，y=2 D．x=﹣3，y=﹣9

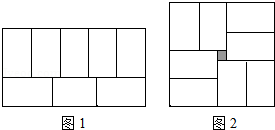5．（2015年•杭州期末）小明在拼图时，发现8个一样大小的长方形，恰好可以拼成一个大的长方形如图（1）；小红看见了，说：“我也来试一试．”结果小红七拼八凑，拼成了如图（2）那样的正方形，中间还留下了一个洞，恰好是边长为3mm的小正方形，则每个小长方形的面积为（　　）

A．120mm² B．135mm²

C．108mm² D．96mm²

6．（2015年•武汉校级期末）从甲地到乙地有一段上坡与一段平路．如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min．设从甲地到乙地上坡与平路分别为xkm，ykm，依题意，所列方程组正确的是（　　）【来源：21·世纪·教育·网】

A． B．

C． D．

7．（潍坊中考）为了研究吸烟是否对肺癌有影响，某肿瘤研究所随机地抽查了10000人，并进行统计分析．结果显示：在吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例是0.5%，吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人．如果设这10000人中，吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意，下面列出的方程组正确的是（　　）21·世纪*教育网

A．

B．

C．

D．

二、填空题

8．（2016年•石狮市期末）方程组经“消元”后可得到一个关于x、y的二元一次方程组为　． 　．21*cnjy*com

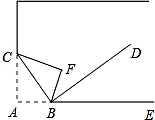
9．（2016年•扶沟县期末）小东将书折过来，该角顶点A落在F处，BC为折痕，如图所示，若DB平分∠FBE，∠DBE比∠CBA大30°，设∠CBA和∠DBE分别为x^°、y°，那么可求出这两个角的度数的方程组是 　．

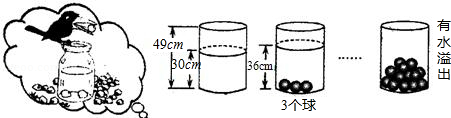
10．（2016年•扶沟县期末）小菲受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作，请根据图中给出的信息，量筒中至少放入　 　小球时有水溢出．【来源：21cnj*y.co*m】

11．（2016年•秦皇岛期末）单项式3x^2m+3ny⁸与﹣2x²y^3m+2n是同类项，则m+n=　 　．【出处：21教育名师】

12．（乌兰察布中考）对于X、Y定义一种新运算“*”：X*Y=aX+bY，其中a、b为常数，等式右边是通常的加法和乘法的运算．已知：3*5=15，4*7=28，那么2*3=　 　．【版权所有：21教育】

13．（2016年•常熟市期末）4个数a，b，c，d排列成，我们称之为二阶行列式．规定它的运算法则为：=ad﹣bc．若=13，则x=　 　．

14．（温州市中考）有一条长度为359mm的铜管料，把它锯成长度分别为59mm和39mm两种不同规格的小铜管（要求没有余料），每锯一次损耗1mm的铜管料，为了使铜管料的损耗最少，应分别锯成59mm的小铜管　 　段，39mm的小铜管　 　段．2-1-c-n-j-y

15．（2015年•白云区期末）某班去看演出，甲种票每张24元，乙种票每张18元，如果35名学生购票恰好用去750元，那么甲种票买了　 　张，乙种票买了

　 　张．

16．（2015年•和平区期末）已知关于x，y的二元一次方程组的解为，那么关于m，n的二元一次方程组的解为　 　．

17．（2015年•武汉校级期末）2015年5月18日华中旅游博览会在汉召开．开幕式上用到甲、乙、丙三种造型的花束，甲种花束由3朵红花、2朵黄花和1朵紫花搭配而成，乙种花束由2朵红花和2朵黄花搭配而成，丙种花束由2朵红花、1朵黄花和1朵紫花搭配而成．这些花束一共用了580朵红花，150朵紫花，则黄花一共用了　 　朵．21教育名师原创作品

三、解答题

18．（2016年•岳池县期末）已知：4x﹣3y﹣6z=0，x+2y﹣7z=0，且x，y，z都不为零．求的值．21*cnjy*com

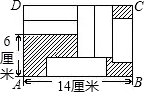
19．（2016年•沛县期末）在矩形ABCD中，放入六个形状、大小相同的长方形，所标尺寸如图所示．试求图中阴影部分的总面积（写出分步求解的简明过程）

20．（2016年•扶沟县期末）解方程组若设（x+y）=A，（x﹣y）=B，则原方程组可变形为，解方程组得，所以解方程组得，我们把某个式子看成一个整体，用一个字母去代替它，这种解方程组的方法叫换元法，请用这种方法解方程组．

21．（2016年•扶沟县期末）已知二元一次方程x+3y=10

（1）直接写出它所有的正整数解；

（2）请你写出一个二元一次方程，使它与已知方程组成的方程组的解为．

22．（武汉市中考）小明家准备装修一套新住房，若甲、乙两个装饰公司，合做需6周完成，需工钱5.2万元；若甲公司单独做4周后，剩下的由乙公司来做，还需9周才能完成，需工钱4.8万元，若只选一个公司单独完成，从节约开支角度考虑，小明家是选甲公司、还是乙公司请你说明理由．www-2-1-cnjy-com

23．（2016年•石景山区期末）在解关于x、y的方程组 时，可以用①×2﹣②消去未知数x，也可以用①×4+②×3消去未知数y，试求a、b的值．

24．（2016年•嘉祥县期末）甲乙两人解方程组．由于甲看错了方程①中的m的值，得到方程组的解为，乙看错了方程②中的n的值，得到方程组的解为，试求m²+n²+mn的值．

25．（2015年•天津期末）已知2台大收割机和5台小收割机同时工作2h共收割小麦3.6hm²，3台大收割机和2台小收割机同时工作5h共收割小麦8hm²．求1台大收割机和1台小收割机每小时各收割小麦多少公顷（hm²）？

（1）分析：如果设1台大收割机每小时各收割小麦x hm²，和1台小收割机每小时各收割小麦y hm²，则2台大收割机和5台小收割机同时工作1h共收割小麦

　 hm²，3台大收割机和2台小收割机同时工作1h共收割小麦　 　hm²（均用含x，y的代数式表示）；21·cn·jy·com

（2）根据以上分析，结合题意，请你列出方程组，求出1台大收割机和1台小收割机每小时各收割小苗多少公顷（hm²）？

26．（2016年•西城区期末）（1）阅读以下内容：

已知实数x，y满足x+y=2，且求k的值．

三位同学分别提出了以下三种不同的解题思路：

甲同学：先解关于x，y的方程组，再求k的值．

乙同学：先将方程组中的两个方程相加，再求k的值．

丙同学：先解方程组，再求k的值．

（2）你最欣赏（1）中的哪种思路？先根据你所选的思路解答此题，再对你选择的思路进行简要评价．

（评价参考建议：基于观察到题目的什么特征设计的相应思路，如何操作才能实现这些思路、运算的简洁性，以及你依此可以总结什么解题策略等等）

请先在以下相应方框内打勾，再解答相应题目．

27．（河南省中考）某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动，收费标准如下：

甲、乙两所学校计划组织本校学生自愿参加此项活动．已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人．经核算，若两校分别组团共需花费20 800元，若两校联合组团只需花费18 000元．

（1）两所学校报名参加旅游的学生人数之和超过200人吗？为什么？

（2）两所学校报名参加旅游的学生各有多少人？

参考答案

一、选择题

1．解：若馒头每个x元，包子每个y元，由题意得：

，

故选：B．

2．解：由题意将代入方程组得：

，

①+②+③得：a+2b+2b+3c+c+3a=2+3+7，

即4a+4b+4c=4（a+b+c）=12，

则a+b+c=3．

故选A．

3．解：设一杯为x，一杯一壶为43元，

则右图为三杯两壶，即二杯二壶+一杯，

即：43×2+x=94

解得：x=8（元）

故选C．

4．解：由题意得，2x﹣y=3，

A、x=5时，y=7，故A选项错误；

B、x=3时，y=3，故B选项错误；

C、x=﹣4时，y=﹣11，故C选项错误；

D、x=﹣3时，y=﹣9，故D选项正确．

故选：D．

5．解：设每个长方形的长为xmm，宽为 ymm，由题意，

得，

解得：．

9×15=135（mm²）．

故选：B．

6．解：设从甲地到乙地上坡与平路分别为xkm，ykm，

由题意得：，

故选：A．

7．解：设吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意得：

．

故选：B．

二、填空题

8．解：，

①+③得x+3y=6④，

由②④组成方程组得．

故答案为．

9．解：设∠CBA和∠DBE分别为x^°、y°，

根据题意，可列方程组：，

故答案为：．

10．解：设放入球后量桶中水面的高度y（cm）与小球个数x（个）之间的一次函数关系式为y=kx+b，由题意，得：，21cnjy.com

解得：，

即y=2x+30；

由2x+30＞49，

得x＞9.5，

即至少放入10个小球时有水溢出．

故答案为：10．

11．解：由题意得：，

①+②得：5m+5n=10，

m+n=2，

故答案为：2．

12．解：∵X*Y=aX+bY，3*5=15，4*7=28，

∴3a+5b=15 ①4a+7b=28 ②，

②﹣①=a+2b=13 ③，

①﹣③=2a+3b=2，

而2*3=2a+3b=2．

13．解：∵=13，

∴（x﹣2）（x﹣2）﹣（x+3）（x+1）=13，

x²﹣4x+4﹣x²﹣4x﹣3=13，

﹣8x=12，

解得，x=﹣，

故答案为：﹣．

14．解：设应分别锯成59mm的小铜管x段，39mm的小铜管y段．

那么损耗的钢管料应是1×（x+y﹣1）=x+y﹣1（mm）．根据题意得：

59x+39y+x+y﹣1=359，

x=6﹣y．

由于x、y都必须是正整数，因此

x=4，y=3，x+y﹣1=6；

x=2，y=6，x+y﹣1=7；

因此据此4段59mm的小钢管最省．

15．解：设甲种票买x张，乙种票买y张，根据题意，得：

，

解得：．

即：甲种票买20张，乙种票买15张．

故选：20；15．

16．解：∵关于x，y的二元一次方程组的解为，

∴，

∴，

解得，

故答案为：．

17．解：设步行街摆放有甲、乙、丙三种造型的盆景分别有x盆、y盆、z盆．

由题意，有，

把②代入①得：x+2y=280．

所以2x+2y+z=（x+z）+（x+2y）=150+280=430（朵）．

即黄花一共用了430朵．

故答案是：430．

三、解答题

18．解：解关于x、y的二元一次方程组得，

把x=3z，y=2z代入得原式==．

19．解：设小长方形的长为x，宽为y，如图可知，

x+3y=14，①

x+y﹣2y=6，即x﹣y=6，②

①﹣②得4y=8，y=2，代入②得x=8，

因此，大矩形ABCD的宽AD=6+2y=6+2×2=10．

矩形ABCD面积=14×10=140（平方厘米），

阴影部分总面积=140﹣6×2×8=44（平方厘米）．

20．解：设x+y=A，x﹣y=B，

方程组变形得：，

整理得：，

①×3+②×2得：13A=156，即A=12，

把A=12代入②得：B=0，

∴，

解得：．

21．解：（1）方程x+3y=10，

解得：x=﹣3y+10，

当y=1时，x=7；当y=2时，x=4；当y=3时，x=1，

则方程的正整数解为；；；

（2）根据题意得：2x+y=0．

22．解：设甲公司单独完成需x周，需要工钱a万元，乙公司单独完成需y周，需要工钱b万元．（1分）

依题意得

解之得

即

经检验：是方程组的根，且符合题意．（4分）

又

解之得（7分）

即甲公司单独完成需工钱6万元，乙公司单独完成需工钱4万元．

答：从节约开支角度考虑，应选乙公司单独完成．（8分）

23．解：由题意可得：，

解之，，

所以a=6，b=．

24．解：根据题意得，4×（﹣3）﹣m（﹣1）=﹣2，5n+5×4=15，

解得m=﹣1，n=10，

把m=﹣1，n=10代入代数式，可得：

原式=91．

25．解：（1）2台大收割机和5台小收割机同时工作1h共收割小麦（2x+5y）hm²，3台大收割机和2台小收割机同时工作1h共收割小麦（3x+2y）hm²；

故答案为（2x+5y），（3x+2y）；

（2）由题意得，

解得．

答：1台大收割机和1台小收割机每小时各收割小麦0.4hm²和0.2hm²．

26．解：我最欣赏（1）中的乙同学的解题思路，

，

①+②得：5x+5y=7k+4，

x+y=，

∵x+y=2，

∴=2，

解得：k=，

评价：甲同学是直接根据方程组的解的概念先解方程组，得到用含k的式子表示x，y的表达式，再代入x+y=2得到关于k的方程，没有经过更多的观察和思考，解法比较繁琐，计算量大；21世纪教育网版权所有

乙同学观察到了方程组中未知数x，y的系数，以及与x+y=2中的系数的特殊关系，利用整体代入简化计算，而且不用求出x，y的值就能解决问题，思路比较灵活，计算量小；21教育网

丙同学将三个方程做为一个整体，看成关于x，y，k的三元一次方程组，并且选择先解其中只含有两个未知数x，y的二元一次方程组，相对计算量较小，但不如乙同学的简洁、灵活．www.21-cn-jy.com

27．解：（1）这两所学校报名参加旅游的学生人数之和超过200人，理由为：

设两校人数之和为a，

若a＞200，则a=18000÷75=240；

若100＜a≤200，则a=18000÷85=211＞200，不合题意，

则这两所学校报名参加旅游的学生人数之和等于240人，超过200人．

（2）设甲学校报名参加旅游的学生有x人，乙学校报名参加旅游的学生有y人，则

①当100＜x≤200时，得

解得（6分）

②当x＞200时，得

解得不合题意，舍去．

答：甲学校报名参加旅游的学生有160人，乙学校报名参加旅游的学生有80人．