28.2解直角三角形（3）

一、选择题

1. 一个人从山下沿30°角的坡路登上山顶,共走了500m,那么这山的高度是 [ ]m.

A.230 B.240 C.250 D.260

2. 一个人从A点出发向北偏东60°方向走了一段距离到达B点，再从B点出发向南偏东15°方向走了一段距离到C点，则∠ABC的度数为 [ ]

A.15° B.75° C.105° D.45°

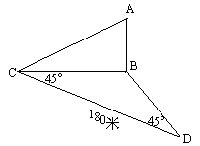
3. 为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是[ ]米

.

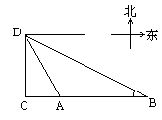
4. 如图,一船向正北航行,看见正东有两个相距10海里的灯塔,船航行半小时后,一个灯塔在船的东南,另一个灯塔在船的东22°30′南,则船的速度(精确到0.1米)是[ ]米/时(tg22°30′=0.4142)

A.12.1 B.13.1 C.14.1 D.15.1

5. 一只船向正东航行,上午7时在灯塔A的正北C处,上午9时到达塔的北偏东60°B处,已知船的速度为每小时20千米,那么AB的距离是[ ]千米.

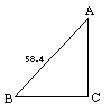
6. 如图：B处有一船,向东航行,上午9时在灯塔A的西南58.4千米的B

上午11时到达灯塔的南C处,那么这船航行的速度是[ ]千米/时.

A.19.65 B.20.65 C.21.65 D.22.65

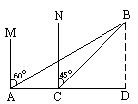
7. 如图：一只船以每小时20千米的速度向正东航行,起初船在A处看见一灯塔B在船的北偏东60°,2小时后,船在C处看见这个灯塔在船的北偏东45°,则灯塔B到船的航海线AC的距离是 [ ]千米.

二、填空题

一只船向东航行,上午9点到一座灯塔的西南68海里处,上午11点到达这座灯塔的正南,这只船航行的速度是_____________.(答案可带根号)

三、解答题

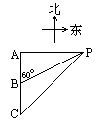
1. 如图：已知一船以每小时20海里的速度向正南行驶,上午10时在A处见灯塔P在正东,1小时后行至B处,观察灯塔P的方向是北60°东.求正午12时船行驶至C处距灯塔P的距离.(答案可带根号)

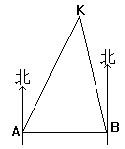
2．如图：东西方向的海岸线上有A、B两码头，相距100 千米，由码头A测得海上船K在北偏东30°，由码头B测得船K在北偏西15°，求船K距海岸线AB的距离（已知tan75°=）

参考答案

一、选择题

1. C 2. B 3. C 4. C 5. D 6. B 7. C

二、填空题

三、解答题

1．

2．千米