第28章锐角三角函数练习题 姓名：________

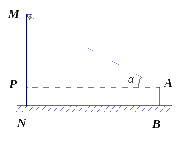
1.（2009年郴州市）如图，数学活动小组来到校园内的一盏路灯下测量路灯的高度，测角仪AB的高度为1.5米，测得仰角为，点B到电灯杆底端N的距离BN为10米，求路灯的高度MN是多少米？（取=1.414，=1. 732，结果保留两位小数）

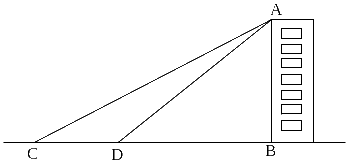
2.(2009成都)某中学九年级学生在学习“直角三角形的边角关系”一章时，开展测量物体高度的实践活动，他们要测量学校一幢教学楼的高度．如图，他们先在点C测得教学楼AB的顶点A的仰角为30°，然后向教学楼前进60米到达点D，又测得点A的仰角为45°．请你根据这些数据，求出这幢教学楼的高度．(计算过程和结果均不取近似值)

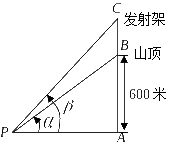
3．（2009年黄石市）三楚第一山——东方山是黄石地区的佛教圣地，也是国家AAA级游览景区．它的主峰海拔约为600米，主峰上建有一座电信信号发射架，现在山脚处测得峰顶的仰角为，发射架顶端的仰角为，其中，求发射架高．

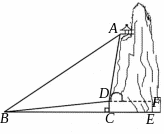
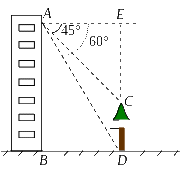
4．(2009年云南省)如图，小芸在自家楼房的窗户A处，测量楼前的一棵树CD的高. 现测得树顶C处的俯角为45°，树底D处的俯角为60°，楼底到大树的距离BD为20米.请你帮助小芸计算树的高度（精确到0.1米）．

5.（2009年济宁市）坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋（公元1112年），为砖彻八角形十三层楼阁式建筑.数学活动小组开展课外实践活动，在一个阳光明媚的上午，他们去测量太子灵踪塔的高度，携带的测量工具有：测角仪．皮尺．小镜子.（1）小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点，用测角仪测出看塔顶的仰角，在点和塔之间选择一点，测出看塔顶的仰角，然后用皮尺量出．两点的距离为m,自身的高度为m.请你利用上述数据帮助小华计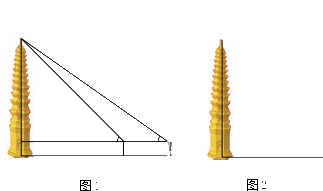 算出塔的高度（，结果保留整数）.

（2）如果你是活动小组的一员，正准备测量塔高，而此时塔影的长为m（如图2）,你能否利用这一数据设计一个测量方案？如果能，请回答下列问题：

①在你设计的测量方案中，选用的测量工具是: ；

②要计算出塔的高，你还需要测量哪些数据？

.[来源:学.科.网]

6．（2009年山东青岛市）在一次数学活动课上，老师带领同学们去测量一座古塔CD的高度．他们首先从A处安置测倾器，测得塔顶C的仰角，然后往塔的方向前进50米到达B处，此时测得仰角，已知测倾器高1.5米，请你根据以上数据计算出古塔CD的高度．

（参考数据：，， ，）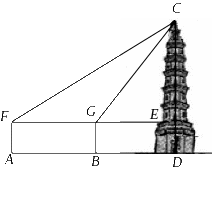

[来源:Z*xx*k.Com]

7．（2009年铁岭市）某旅游区有一个景观奇异的望天洞，点是洞的入口，游人从入口进洞游览后，可经山洞到达山顶的出口凉亭处观看旅游区风景，最后坐缆车沿索道返回山脚下的处．在同一平面内，若测得斜坡的长为100米，坡角，在处测得的仰角，在处测得的仰角，过点作地面的垂线，垂足为．（1）求的度数；（2）求索道的长．（结果保留根号）

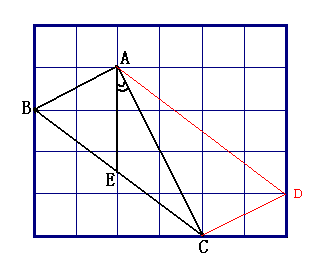
8.（2009年福州）如，在边长为1的小正方形组成的网格中，的三个顶点均在格点上，请按要求完成下列各题：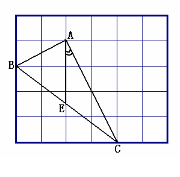

（1）用签字笔画AD∥BC（D为格点），连接CD；

（2）线段CD的长为 ；

（3）请你在的三个内角中任选一个锐角，若你所选的

锐角是 ，则它所对应的正弦函数值是 ．

（4） 若E为BC中点，则tan∠CAE的值是 .

9．（2009年日照）如图，斜坡AC的坡度（坡比）为1:，AC＝10米．坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求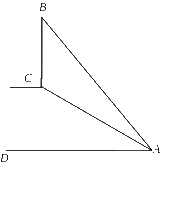 旗杆BC的高度．

10．（2009贺州）如图，，矩形ABCD的对角线，边BC在OM上，当AC=3时，AD长是多少？（结果精确到0.01）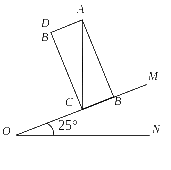

11.（2009年天津市）在一次课外实践活动中，同学们要测量某公园人工湖两侧两个凉亭之间的距离．现测得m，m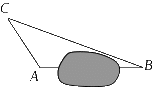， ，请计算两个凉亭之间的距离．

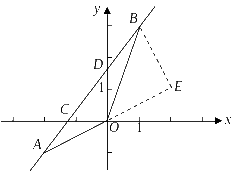
12. （ 2009年嘉兴市）如图，已知一次函数的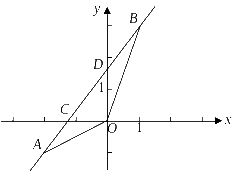 图象经过，两点，并且交x轴于点C，交y轴于点D，（1）求该一次函数的解析式；

（2）求的值；（3）求证：．

[来源:Z#xx#k.Com]

13. （2009年泸州）如图11，在△ABC中，AB=BC，以AB为直径的⊙O与AC交于点D，过D作DF⊥BC， 交AB的延长线于E，垂足为F．

(1)求证：直线DE是⊙O的切线；(2)当AB=5，A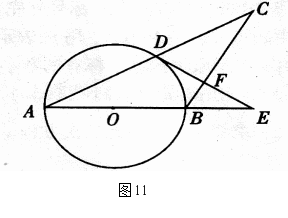 C=8时，求cosE的值．

14.（2009呼和浩特）要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角一般满足．如图，现有一个长6m的梯子，梯子底端与墙角的距离为3m．（1）求梯子顶端距离墙角的距离．（结果精确到0.1m）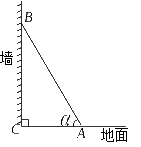

（2）计算此时梯子与地面所成角，并判断人能否安全使用这个梯子．

（，）

15.（2009年郴州市）如图，数学活动小组来到校园内的一盏路灯下测量路灯的高度，测角仪AB的高度为1.5米，测得仰角为，点B到电灯杆底端N的距离BN为10米，求路灯的高度MN是多少米？（取=1.414，=1.732，结果保留两位小数）

16.（2009年常德市）如图，某人在D处测得山顶C的仰角为30^o，向前走200米来到山脚A处，测得山坡AC的坡度为i=1∶0.5，求山的高度（不计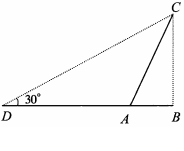 测角仪的高度，，结果保留整数）．

17.（2009年包头）如图，线段分别表示甲．乙两建筑物的高，，从点测得点的仰角为60°从点测得点的仰角为30°，已知甲建筑物高米．（1）求乙建筑物的高；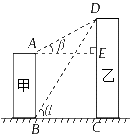

（2）求甲．乙两建筑物之间的距离（结果精确到0.01米）．

（参考数据：）

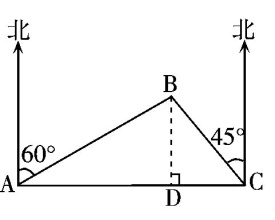
18．（2009眉山）海船以5海里/小时的速度向正东方向行驶，在A处看见灯塔B在海船的北偏东60°方向，2小时后船行驶到C处，发现此时灯塔B在海船的北偏西45方向，求此时灯塔B到C处的距离．

19.（2009年台州市）如图，有一段斜坡长为10米，坡角，为方便残疾人的轮椅车通行，现准备把坡角降为5°． （1）求坡高;

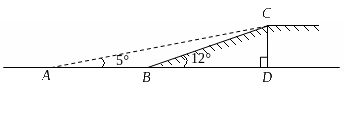（2）求斜坡新起点与原起点的 距离（精确到0.1米）．

2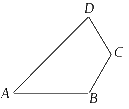 0．（2009年赤峰市）公园里有一块形如四边形ABCD的草地，测得BC=CD=10米，∠B=∠C=120°，∠A=45°．请你求出这块草地的面积.

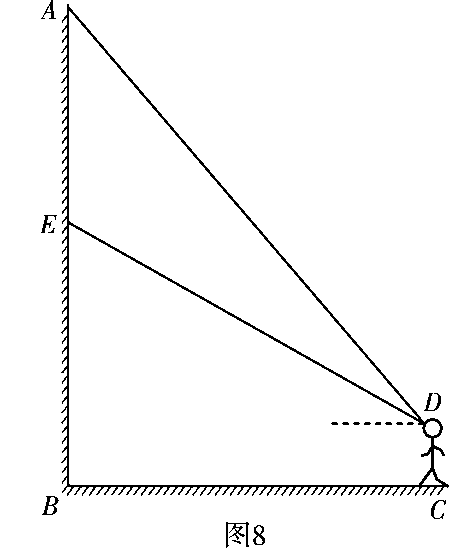
21.（2009年娄底）在学习实践科学发展观的活动中，某单位在如图8所示的办公楼迎街的墙面上垂挂一长为30米的宣传条幅AE，张明同学站在离办公楼的地面C处测得条幅顶端A的仰角为50°，测得条幅底端E的仰角为30°. 问张明同学是在离该单位办公楼水平距离多远的地方进行测量？（精确到整数米）

（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20，sin30°=0.50，cos30°≈0.87，tan30°≈0.58）

22. (2009年金华市) 如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部，形成一个斜坡，货物通过斜坡进行搬运.根据经验，木板与地面的夹角为20°（即图2中∠ACB=20°）时最为合适，已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度（参考数据：sin20°≈0.3420,cos20°≈0.9397,精确到0.1m）.

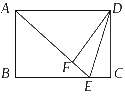
24.（2009重庆綦江）如图，在矩形ABCD中，是边上的点，AE=BC，DF⊥AE，垂足为F，连接DE． （1）求证：；

（2）如果，求的值．

第28章锐角三角函数练习题参考答案

1. 解：在直角三角形中，，米

米

因为米

所以米

答：路灯的高度为7.27米

2.解：如图，由已知可得∠ACB=30°，∠ADB=45°

∴在Rt△ABD中，BD=AB

又在Rt△ABC中，∵ tan30°=

∴，即BC=AB

∵BC=CD+BD，∴AB=CD+AB

即（-1）AB=60

∴AB==30(+1)米

∴教学楼高度为30(+1)米.

3. 解：在中，

∵，

∴．

在中，

∵，

∴．

∴．

答：发射架高为25m．

4. 解：过点A作AE∥BD交DC的延长线于点E，

则∠AEC=∠BDC=90°．

∵，，

∴．

∵，

∴，

　（米）．

答：树高约为米．

5. 解:（1）设的延长线交于点，长为，则.

∵,∴.∴.

∵,∴,解得.

∴太子灵踪塔的高度为.

(2) ①测角仪．皮尺； ② 站在P点看塔顶的仰角．自身的高度.

6. 解：由题意知，，

∴，设，

在中，

，则；

在中，

，

则；

∵，

∴．

，

∴（米）．

答：古塔的高度约是39米．

7. （1）解：∵，∴．

又∵，

∴，

∵，

∴．

（2）过点作于点．

在中，，

∴

又∵，

∴．

．

在中，

∴，

∴ （米）

答：索道长米．

8. （1）如图 （2）;

（3）∠CAD，(或∠ADC，); （4）.

9. 延长BC交AD于E点，则CE⊥AD．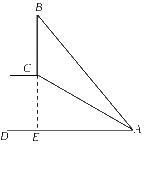

在Rt△AEC中，AC＝10，

由坡比为1: 可知：∠CAE＝30°，

∴ CE＝AC·sin30°＝10× ＝5，

AE＝AC·cos30°＝10× ＝5 ．

在Rt△ABE中，

BE＝＝=11．

∵ BE＝BC＋CE，

∴ BC＝BE－CE＝11-5＝6（米）．

答：旗杆的高度为6米．

10. 解：延长AC交 ON于点E，

∵AC⊥ON，

∠OEC=90°，

∵四边形ABCD是矩形，

∴∠ABC=90°，AD=BC，

又∵∠OCE=∠ACB，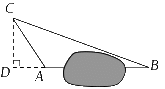

∴∠BAC=∠O=25°，

在Rt△ABC中，AC=3，

∴BC=AC·sin25°≈1.27

∴AD≈1.27

11. 如图，过点作垂直于交的延长线于点.在中，.∴，=15.又在中，，.，答：两个凉亭之间的距离为50m.

12. （1）由，解得，所以　

（2），．

在△OCD中，，，

∴．　

（3）取点A关于原点的对称点，

则问题转化为求证．

由勾股定理可得，

，，，

∵，

∴△EOB是等腰直角三角形．

∴．　

∴．

13.

14. 解：（1）在中，

（2）在中，

可以安全使用.

15.. 解：在直角三角形中，，米

米

因为米

所以米

答：路灯的高度为7.27米

16. 设山高BC =，则AB=，

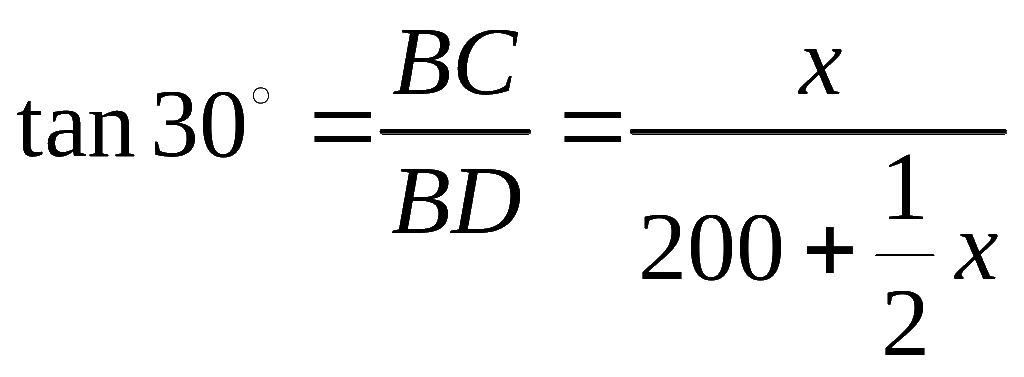由，得

，

解得米

17.解：（1）过点作于点，

根据题意，得，

米，

设，则，

在中，，

，

在中， ，

（米）．

（2），，

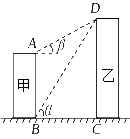（米）．

18. 解：如图，过B点作BD⊥AC于D

∴∠DAB＝90°－60°＝30°，∠DCB＝90°－45°＝45° [来源:Zxxk.Com]

设BD＝x,在Rt△ABD中，AD＝tan30°＝

在Rt△BDC中,BD＝DC＝x BC＝

又AD＝5×2＝10 ∴得

∴（海里）

答：灯塔B距C处海里

19. 解：（1）在中，

（米）．

（2）在中，

（米）；

在中， （米），

（米）．

答：坡高2.1米，斜坡新起点与原起点的距离为13.5米

20解：连接，过作于，

，

．

．

．

.21. 解：方法一：过D点作DF⊥AB于F点

在Rt△DEF中，设EF=x，则DF=x

在Rt△ADF中，tan50°=≈1.204分

30+x=x×1.20

x≈27.8 

∴DF=x≈48 

答：张明同学站在离办公楼约48米处进行测量的

方法二：过点D作DF⊥AB于F点 

在Rt△DEF中，EF=FD·tan30°

在Rt△AFD中，AF=FD·tan30°

∵AE+EF=AF

∴30+FDtan30°=FD·tan50°

∴FD≈48

答：张明同学站在离办公楼约48米处进行测量的

22. 解：由题意可知：AB⊥BC

∴在Rt△ABC中, sin∠ACB=　

∴AC= = = ≈4.39m

∴CD = AC+AD= 4.39+0.5 = 4.89 ≈ 4.9m

答：木板的长度约为4.9m

23. （1）证明：在矩形中，

．

（2）解：由（1）知

在直角中，

_{[来源:Z&xx&k.Com]}

在直角中，

．