w ww.ks5u.com

第5节　反冲运动　火箭

1．一个静止的物体在______的作用下分裂为两个部分，一部分向某一个方向运动，另一

部分必然向______的方向运动的现象称为反冲运动．

(1)物体的不同部分在____力作用下向相反方向运动．

(2)反冲运动中，相互作用力一般较大，通常可以用______________来处理．

(3)反冲运动中，由于有__________能转变为______能，所以系统的总动能________．

(4)反冲现象的应用及防止

①应用：农田、园林的喷灌装置是利用反冲使水从喷口喷出时，一边喷水一边______．

②防止：用枪射击时，由于枪身的反冲会影响射击的________，所以用步枪射击时要把

枪身抵在__________，以减少反冲的影响．

2．利用______运动，火箭燃料燃烧产生的高温、高压燃气从尾喷管迅速喷出时，使火箭

获得巨大的______，这就是火箭的工作原理．

影响火箭获得速度大小的因素有：

(1)喷气速度：现代液体燃料火箭的喷气速度约为2 000 m/s～4 000 m/s.

(2)火箭的质量比：指火箭起飞时的质量与火箭除燃料外的箭体______之比．喷气速度

______，质量比______，火箭获得的速度越大．

3．下列属于反冲运动的是(　　)

A．喷气式飞机的运动 B．直升飞机的运动

C．火箭的运动 D．反击式水轮机的运动

4．假定冰面是光滑的，某人站在冰冻河面的中央，他想到达岸边，则可行的办法是(　　)

A．步行 B．挥动双臂

C．在冰面上滚动 D．脱去外衣抛向岸的反方向

5．采取下列措施有利于增大喷气式飞机的飞行速度的是(　　)

A．使喷出的气体速度更大

B．使喷出的气体温度更高

C．使喷出的气体质量更大

D．使喷出的气体密度更小

6．一静止的质量为M的原子核，以相对于地的水平速度v放射出一质量为m的粒子后，

原子核剩余部分反冲运动的速度大小为(　　)

A. B.

C.v D.v

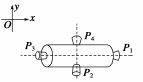
图1

7．如图1所示为一空间探测器的示意图，P₁、P₂、P₃、P₄是四个喷气发动机，P₁、P₃

的连线与空间一固定坐标系的x轴平行，P₂、P₄的连线与y轴平行，每台发动机开动时，

都能向探测器提供推力，但不会使探测器转动，开始时，探测器以恒定的速率v₀向x轴

正方向平动，要使探测器改为向x轴正向偏y轴负向60°的方向以原来的速率v₀平动，

则可(　　)

A．先开动P₁适当时间，再开动P₄

B．先开动P₃适当时间，再开动P₂

C．先开动P₄适当时间，再开动P₂

D．先开动P₃适当时间，再开动P₄

【概念规律练】

知识点一　反冲现象

1．一颗质量为0.02 kg的子弹以2 700 m/s的速度从枪口射出，枪身的质量为7.5 kg，若

枪是自由放置的，设子弹射出的方向为正方向，则枪的反冲速度是________m/s.

2．一门旧式大炮，炮身的质量M＝1 000 kg，水平发射一枚质量是2.5 kg的炮弹．如果

炮弹从炮口飞出时的速度是600 m/s，求炮身后退的速度大小．

知识点二　火箭的运动

3．运送人造地球卫星的火箭开始工作后，火箭做加速运动的原因是(　　)

A．燃料推动空气，空气的反作用力推动火箭

B．火箭发动机将燃料燃烧产生的气体向后迅速喷出，气体的反作用力推动火箭

C．火箭吸入空气，然后向后排出，空气对火箭的反作用力推动火箭

D．火箭燃料燃烧发热，加热周围空气，空气膨胀推动火箭

4．火箭发动机每次喷出m₀＝200 g的气体，喷出的气体相对于地面的速度为v＝1 000

m/s，设火箭的初质量M＝300 kg，发动机每秒喷气20次，在不考虑地球引力及空气阻

力的情况下，火箭在1 s末的速度为多大？

【方法技巧练】

一、用“人船模型”分析实际问题

图2

5．如图2所示，长为l、质量为M的小船停在静水中，一个质量为m的人站在船头，

若不计水的黏滞阻力，当人从船头走到船尾的过程中，船和人对地面的位移各是多少？

6．质量为M的热气球吊筐中有一质量为m的人，共同静止在距地面为h的高空中．现

从气球上放下一根质量不计的软绳，为使此人沿软绳能安全滑到地面，则软绳至少有多

长？

二、利用动量守恒、机械能守恒解决反冲运动问题的方法

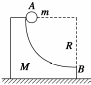
图3

7．如图3所示，带有光滑的半径为R的1/4圆弧轨道的滑块静止在光滑水平面上，滑块

的质量为M.使一质量为m的小球由静止从A点沿圆弧轨道释放，当小球从B点水平飞

出时，滑块的速度为多大？

图4

1．小车上装有一桶水，静止在光滑水平地面上，如图4所示，桶的前、后、底及侧面各

装有一个阀门，分别为S₁、S₂、S₃、S₄(图中未全画出)．要使小车向前运动，可采用的方

法是(　　)

A．打开阀门S₁ B．打开阀门S₂

C．打开阀门S₃ D．打开阀门S₄

2．静止的实验火箭，总质量为M，当它以对地速度v₀喷出质量为Δm的高温气体后，

火箭的速度为(　　)

A. B．－

C. D．－

3．一小型火箭在高空绕地球做匀速圆周运动，若其沿运动方向的相反方向释放出一物体

P，不计空气阻力，则(　　)

A．火箭一定离开原来轨道运动

B．物体P一定离开原来轨道运动

C．火箭运动半径一定增大

D．物体P运动半径一定减小

4．一航天器完成对月球的探测任务后，在离开月球的过程中，由静止开始沿着与月球表

面成一倾角的直线飞行，先加速运动，再匀速运动，探测器通过喷气而获得推动力，以

下关于喷气方向的描述中正确的是(　　)

A．探测器加速运动时，沿直线向后喷气

B．探测器加速运动时，竖直向下喷气

C．探测器匀速运动时，竖直向下喷气

D．探测器匀速运动时，不需要喷气

5．如图5所示，

图5

自行火炮(炮管水平)连同炮弹的总质量为M，在水平路面上以v₁的速度向右匀速行驶，

发射一枚质量为m的炮弹后，自行火炮的速度变为v₂，仍向右行驶，则炮弹相对炮筒的

发射速度v₀为(　　)

A.

B.

C.

D.

6．一个质量为M的平板车静止在光滑的水平面上，在平板车的车头与车尾站着甲、乙

两人，质量分别为m₁和m₂，当两人相向而行时(　　)

A．当m₁>m₂时，车子与甲运动方向一致

B．当v₁>v₂时，车子与甲运动方向一致

C．当m₁v₁＝m₂v₂时，车子静止不动

D．当m₁v₁>m₂v₂时，车子运动方向与乙运动方向一致

7.质量为M的玩具汽车拉着质量为m的小拖车，在水平地面上以速度v匀速前进，某一

时刻拉拖车的线突然断了，而小汽车的牵引力不变，汽车和拖车与地面间的动摩擦因数

相同，一切阻力也不变．则在拖车停止运动时，汽车的速度大小为________．

图6

8．一旧式高射炮的炮筒与水平面的夹角为α＝60°，当它以v₀＝100 m/s的速度发射出炮

弹时，炮车反冲后退，已知炮弹的质量为m＝10 kg，炮车的质量M＝200 kg，炮车与地

面间的动摩擦因数μ＝0.2，如图6所示．则炮车后退多远停下来？(取g＝10 m/s²)

图7

9．如图7所示，一个质量为m的玩具蛙，蹲在质量为M的小车的细杆上，小车放在光

滑的水平桌面上，若车长为L，细杆高为h且位于小车的中点，试求：当玩具蛙至少以

多大的水平速度v跳出，才能落到桌面上．

10.在沙堆上有一木块，质量m₁＝5 kg，木块上放一爆竹，质量m₂＝0.1 kg.点燃爆竹后，

木块陷入沙中深度为d＝5 cm，若沙对木块的平均阻力为58 N，不计爆竹中火药的质量

和空气阻力，求爆竹上升的最大高度．

11．课外科技小组制作了一只“水火箭”，用压缩空气压出水流使火箭运动．假如喷出

的水流流量保持为2×10^－4 m³/s，喷出速度保持为对地10 m/s.启动前火箭总质量为1.4

kg，则启动2 s末火箭的速度可以达到多少？已知火箭沿水平轨道运动，阻力不计，水

的密度是1×10³ kg/m³.

第5节　反冲运动　火箭

课前预习练

1．内力　相反　(1)内　(2)动量守恒定律　(3)其他形式　动　增加　(4)①旋转　②准确性　肩部

2．反冲　速度　(2)质量　越大　越大

3．ACD　[反冲现象是一个物体分裂成两部分，两部分朝相反的方向运动，故直升飞机不是反冲现象．]

4．D　[因为冰面光滑，无法行走和滚动，由动量守恒定律知，只有抛出物体获得反冲速度才能到达岸边．]

5．AC　[由动量守恒得mv＝(M－m)v′，v′＝.]

6．B

7．A　[探测器原来沿着x轴正方向以速率v₀飞行，具有的动量为mv₀，方向沿x轴正方向．如要通过操作P₁、P₂、P₃、P₄四个喷气发动机，利用反冲使得探测器仍以速率v₀沿着x轴正向偏y轴负向60°的方向，即探测器动量的x分量由mv₀变为mv₀cos 60°＝mv₀，而y分量由0变为－mv₀sin 60°＝－mv₀，根据反冲规律及动量定理可判定，为了使探测器运动转向，必须要开动x轴正方向喷气的发动机P₁一段时间，以使探测器动量的x分量由mv₀变为mv₀，再开动向y轴正方向喷气的P₄一段时间，以使探测器动量的y分量由0变为－mv₀.]

课堂探究练

1．－7.2

解析　把子弹和枪看成一个系统，动量守恒，设枪和子弹的质量分别为M和m，速度分别为v₁，v₂，则由动量守恒定律得Mv₁＋mv₂＝0，得v₁＝－＝－7.2 m/s.

2．见解析

解析　把炮弹和炮身看成一个系统，在发射炮弹时，炸药爆炸产生的推力远大于炮身所受到的地面的摩擦力，因此系统水平方向动量守恒．设炮身和炮弹的质量分别为M和m，炮弹飞出时的速度为v，此时炮身的速度为u，则在水平方向上根据动量守恒定律有mv＋Mu＝0，得u＝－＝－ m/s＝－1.5 m/s，负号表示炮身的速度方向与炮弹射出的方向相反．

方法总结　(1)反冲运动初状态系统的总动量一般为零．(2)列标量方程m₁v₁＝m₂v₂或矢量方程m₁v₁＋m₂v₂＝0求解．

3．B　[火箭的工作原理是利用反冲运动，是火箭燃料燃烧产生的高温高压燃气从尾喷管迅速喷出时，使火箭获得反冲速度，故正确答案为B.]

点评　本题考查了火箭的工作原理，要注意与火箭发生相互作用的是火箭喷出的燃气，不是外界的空气．而与带螺旋桨的直升机发生相互作用的才是空气，应注意两者的区别．

4．13.5 m/s

解析　设火箭1 s末的速度为v₁，由于忽略了万有引力和阻力，所以动量守恒，以火箭飞行的方向为正方向，0＝(M－20m₀)v₁－20m₀v，v₁＝＝ m/s≈13.5 m/s

5．见解析

解析　设某一时刻人对地的速度为v₂，船对地的速度为v₁，选人前进的方向为正方向，根据动量守恒定律有：mv₂－Mv₁＝0，即＝.因为在人从船头走到船尾的整个过程中，每一时刻系统都满足动量守恒，所以每一时刻人的速度与船的速度之比，都与它们的质量成反比，从而可以得出判断：在人从船头走到船尾的过程中，人的位移x₂与船的位移x₁之比，也等于它们的质量的反比，即＝.此式是人船模型的位移与质量的关系式，此式的适用条件是：一个原来静止的系统，在系统内发生相对运动的过程中，有一个方向的动量守恒(如水平方向或竖直方向)．使用这一关系式时应注意：x₁和x₂是相对同一参考系的位移．由图可以看出：x₁＋x₂＝l，＝，所以x₁＝l，x₂＝l.

6．见解析

解析　

设绳梯长为L，人沿软绳滑至地面的时间为t，由图可知，L＝x_人＋x_球．设人下滑的平均速度为v，气球上升的平均速度为u，由动量守恒定律，有0＝Mu－mv，即0＝M－m()，0＝Mx_球－mx_人，又有x_人＋x_球＝L，x_人＝h，由各式可得L＝h.

7．答案　m

解析　设小球从B点飞出时速度为v₁，滑块的速度为v₂，有

mv₁－Mv₂＝0

mgR＝mv＋Mv

解得v₂＝m

思路点拨　运动过程中小球的机械能不守恒，但小球和滑块组成的系统机械能守恒，又因为系统在水平方向不受外力，故系统水平方向的动量守恒．

点评　小球在下滑过程中，滑块对小球的支持力、小球对滑块的压力都是内力，系统水平方向不受外力，故水平方向系统的动量守恒，但由于滑块的后退，滑块对小球的支持力和小球的运动方向并不垂直，除重力对小球做功外，支持力对小球也做功，所以小球的机械能并不守恒，但小球和滑块这一系统由于无机械能与其他形式的能的转化，所以系统的机械能守恒．

课后巩固练

1．B

2．B　[由动量守恒定律得Δmv₀＋(M－Δm)v＝0.火箭的速度为v＝－.选项B正确．]

3．AC　[由反冲运动的知识可知，火箭的速度一定增大，火箭做离心运动，运动半径增大．但物体P是否离开原来的轨道运动，要根据释放时的速度大小而定，若释放时的速度与原来的速度大小相等，则P仍在原来的轨道上反方向运动．]

4．C　[由题意知，航天器所受重力和推动力的合力沿飞行的直线方向．故只有选项C正确．]

5．B　[自行火炮水平匀速行驶时，牵引力与阻力平衡，系统动量守恒，设向右为正方向，发射前总动量为Mv₁，发射后系统的动量之和为(M－m)v₂＋m(v₀＋v₂)，则由动量守恒定律可得：Mv₁＝(M－m)v₂＋m(v₀＋v₂)

解得v₀＝－v₂＝.]

6．CD　[甲、乙和平板车组成的系统在水平方向动量守恒，设甲运动的方向为正方向，有0＝m₁v₁－m₂v₂＋Mv.可见当m₁v₁＝m₂v₂时，v＝0，即车子静止不动，C正确；当m₁v₁>m₂v₂时，v<0，即车子与乙运动方向相同，D正确．]

7.v

解析　由于汽车和拖车组成的系统所受的牵引力和阻力始终是一对平衡力，故系统的动量守恒，由(M＋m)v＝Mv′，得v′＝v.

8．1.56 m

解析　以炮弹和炮车组成的系统为研究对象，在发射炮弹过程中系统在水平方向动量守恒，设炮车获得的反冲速度为v，以v₀的水平分速度方向为正方向，有

mv₀cos α－Mv＝0

得v＝＝ m/s＝2.5 m/s

由牛顿第二定律得炮车后退的加速度为

a＝＝μg＝2 m/s²

由运动学公式得炮车后退的距离为：

x＝＝ m≈1.56 m.

9.

解析　蛙跳出后做平抛运动，运动时间为t＝，蛙与车水平方向动量守恒，由动量守恒定律得Mv′－mv＝0，若蛙恰好落在桌面上，则有v′t＋vt＝，上面三式联立可求出v＝ .

10．20 m

解析　爆竹爆炸时系统内力远大于外力，竖直方向动量守恒，取向上为正方向，则

0＝m₂v－m₁v′，①

木块陷入沙中的过程做匀减速运动直到停止，由动能定理得(F_f－m₁g)d＝m₁v′²②

解得v′＝0.4 m/s，

代入①式，得v＝v′＝20 m/s

爆竹以速度v做竖直上抛运动，上升的最大高度为

h＝＝20 m

11．4 m/s

解析　“水火箭”喷出水流做反冲运动．设火箭原来总质量为M，喷出水流的流量为Q，水的密度为ρ，水流的喷出速度为v，火箭的反冲速度为v′，由动量守恒定律得

(M－ρQt)v′＝ρQtv

火箭启动2 s末的速度为

v′＝＝ m/s＝4 m/s