第五章《相交线与平行线》水平测试题

班级 学号 姓名 成绩

一、填空题（每小题3分，共30分）

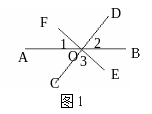
1.如图1,直线AB、CD、EF相交于O，∠1=40°，∠2=60°，则∠3= .

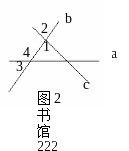
2.如图2，直线a，b，c两两相交，∠1=80°，∠2=2∠3，则∠4= .

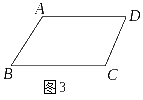
3.如图3，已知∠A=75°，∠B=105° 则＿＿＿＿＿∥＿＿＿＿＿＿＿.

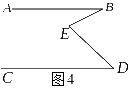
4.如图4，已知AB∥CD，∠B=30°，∠D=40°，则∠E=＿＿＿＿＿度.

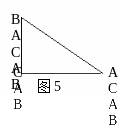
5.如图5，AC⊥BC, 且BC=5，AC=12，AB=13，则点A到BC的距离是 点B到点A的距离是 .

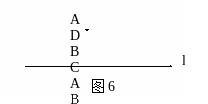
6.如图6，现有一条高压线路沿公路l旁边建立，某村庄A需进行农网改造，必须要从这条高压线上架接一条线路去村庄A，为了节省费用，请你帮他们规划一下，并说明理由.理由是

7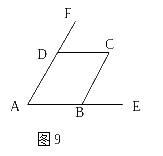 .如图7，AB、CD相交于O，OE、OF分别是∠AOD和∠BOD的平分线，试判断直线OE、OF的位置关系_________.

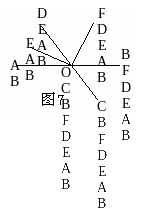
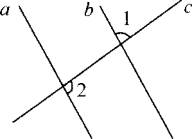
图8

8.如图8，两条直线a、b被第三条直线c所截，如果a∥b，∠1=70°，则∠2=______.

9.如图9，AB∥CD，AD∥BC，则图中与∠A相等的角有_____个.

10．在直线AB上任取一点O，过点O作射线OC、OD，使OC⊥OD，当∠AOC=30°时，∠BOD的度数是 ．

二、选择题 (每小题3分，共18分)

11. 下列说法正确的是（ ）

A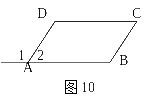 .同一个平面内，不相交的两条线段是平行线B.同一个平面内，两条直线不相交就重合

C.同一个平面内，没有公共点的两条直线是平行线D.不相交的两条直线是平行线

12. 已知两直线相交, 则下列结论成立的是 ( )

A．所构成的四个角中,有一个角是直角 B. 四个角都相等

C． 相邻的两个角互补 D. 对顶角互补

13.如图10，已知∠1=∠B，∠2=∠C，则下列结论不成立的是( )

A． AD∥BC B.∠B=∠C

C．∠2+∠B=180° D.AB∥CD

14．下列图形中，由AB∥CD，能得到∠1=∠2，的是（ ）

1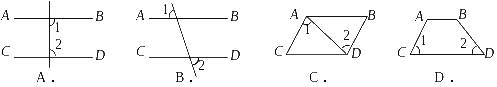 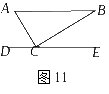5．如图11， 中，∠ACB=90°，DE 过点C，且DE∥AB，若∠ACD=55°，则∠B的度数是（ ）

A．35° B．45° C．55° D．65°

16. 下列说法中，正确的个数为（ ）

(1)过一点有无数条直线与已知直线平行

（2）如果a∥b，a∥c，那么b∥c

（3如果两线段不相交，那么它们就平行 （4）如果两直线不相交，那么它们就平行

A.1个 B.2个 C.3个 D.4个

三、根据下列证明过程填空（每空1分，共18分）

1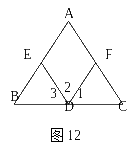 7.如图12，(1)因为∠A=_____(已知)，

所以AC∥ED( )

(2)因为∠2=_____(已知)，

所以AC∥ED( )

(3)因为∠A+_____=180°(已知)，

所以AB∥FD( )

(4)因为AB∥_____(已知)，

所以∠2+∠AED=180°( )

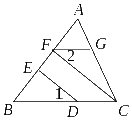( 5)因为AC∥_____(已知)，

所以∠C=∠3( )

18．如图13，∠1=∠2 ，CF⊥AB ，DE⊥AB ，求证：FG∥BC

证明：因为 CF⊥AB ，DE⊥AB （　　　　　）

所以 ∠BED=90° ，∠BFC=90°（ ）

所以 ∠BED=∠BFC （ ）

所以 ED∥FC （ ）

所以 ∠1=∠BCF （ ）

因为 ∠2=∠1 （ ）

所

图13

所以 FG∥BC （ ）

四、解答题

19．画图题：

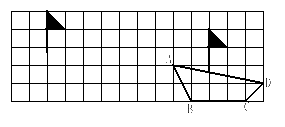
把小船ABCD通过平移后到 的位置，请你根据题中信息，画出平移后的小船位置．(5分)

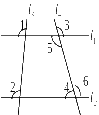
20．如图：已知∠1+∠2=180° , ∠3=110°， 求∠4的度数.(7分)

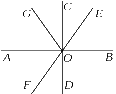
21．如图：AB，CD，EF相交于O点，AB⊥CD，OG平分∠AOE，∠FOD=30°，求∠BOE及∠AOG的度数.(8分)

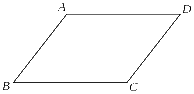
22．如图：已知AB∥DC ，AD∥BC ，求证：∠B=∠D (8分)

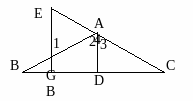
23．如图，AD⊥BC于D,EG⊥BC于G，∠E=∠1，那么AD平分∠BAC吗?

试说明理由(8分)

参考答案：

一、填空题

1．80°提示：从图上可以知道∠1+∠2+∠3=180°，所以∠3=80°

2．140°提示：∠1与∠2是对顶角，所以∠2=80°，又因为∠2=2∠3，所以∠3=40°，又因为∠4=180°-∠3，所以∠4=140°

3．AD∥BC 提示：因为∠A+∠B=180⁰，所以AD∥BC

4．70°提示：过点E作EF根据平行线的性质可知∠BED=∠BEF+∠FED=∠B+∠D=70°.

5．AC，AB∥AB，

6．作图：过点A作l的垂线段最短.

7．垂直

8．110°

9．3个 提示：分别是∠FDC，∠C，∠CBE.

10．60°或120° 提示：点C与D在AB的同侧或异侧两种情况.

二、选择题

11．C

12．C 提示：只有当两直线垂直时A、B、D才成立.

13．B提示：∠1=∠B可得AD∥BC，∠2+∠B=180°根据∠C=∠2可得AD∥BC故选B

14．B

15．A提示：DE∥AB所以∠B=∠BCE，所以∠B=180°-90°-55°=35°

16．A 提示：只有（2）对

三、根据下列证明过程填空

17．（1）∠BED 同位角相等，两直线平行（2）∠DFC 内错角相等，两直线平行（3）∠AFD同旁内角互补，两直线平行（4）DF 两直线平行，同旁内角互补（5）ED 两直线平行，同位角相等

18．已知，等式的性质，等量代换，同位角相等，两直线平行，两直线平行，同位角相等，已知，等量代换，内错角相等，两直线平行

四、解答题

19．将小船向左移9个格子，再向上移1个格子（画图略）

20．解：因为∠1+∠2=180°

所以l₁∥l₂

所以∠3=∠6

又因为∠4+∠6=180°

所以∠4=180°-∠3

又因为∠3=110°

所以∠4=70°

21．解：因为∠FOD=30°，∠COE与∠FOD是对顶角，所以∠EOC=30°

因为AB⊥CD所以∠BOC=90°，∠BOE=∠BOC -∠EOC =60°

因为∠AOE=90°+∠EOC=120°且OG平分∠AOE所以∠AOG=60°

22．解：因为AB∥DC（已知）

所以∠B+∠C=180°（两直线平行，同旁内角互补）

因为AD∥BC（已知）

所以∠D+∠C=180°（两直线平行，同旁内角互补）

所以∠B=∠D（等角的补角相等）

23．解：AD平分∠BAC

理由：因为AD⊥BC于D,EG⊥BC于G

所以EG∥AD（垂直于同一条直线的两直线平行）

所以∠1=∠2（两直线平行，内错角相等）

∠E=∠3（两直线平行，同位角相等）

又因为∠E=∠1

所以∠3=∠2（等量代换）

所以AD平分∠BAC（角平分的定义）