A．（a﹣b）2=a2﹣b2 B．3ab﹣ab=2ab C．a（a2﹣a）=a2 D．人教版八年级数学上册
14.1.4.2《单项式乘以多项式》同步训练习题（学生版）
一．选择题
1．（2015•黔东南州）下列运算正确的是（ ）
A．（a﹣b）2=a2﹣b2 B．3ab﹣ab=2ab C．a（a2﹣a）=a2 D．
2．（2015春•岱岳区期末）如果长方体的长为3a﹣4，宽为2a，高为a，则它的体积是（ ）
A．3a2﹣4a B．a2 C．6a3﹣8a2 D．6a2﹣8a
3．（2015秋•重庆校级月考）化简x（2x﹣1）﹣x2（2﹣x）的结果是（ ）
A．﹣x3﹣x B．x3﹣x C．﹣x2﹣1 D．x3﹣1
4．（2015秋•遂宁校级月考）若三角形的底边为2m+1，高为2m，则此三角形的面积为（ ）
A．4m2+2m B．4m2+1 C．2m2+m D．2m2+m
5．（2014春•南海区校级期中）下列计算正确的是（ ）
A．（﹣2a）•（3ab﹣2a2b）=﹣6a2b﹣4a3b
B．（2ab2）•（﹣a2+2b2﹣1）=﹣4a3b4
C．（abc）•（3a2b﹣2ab2）=3a3b2﹣2a2b3
D．（ab）2•（3ab2﹣c）=3a3b4﹣a2b2c
6．（2013秋•鲤城区校级期末）三个连续的奇数，若中间一个为a，则它们的积为（ ）
A．a3﹣4a B．a3﹣6a C．4a3﹣a D．4a3﹣6a
7．（2013秋•合浦县期末）今天数学课上，老师讲了单项式乘以多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：﹣3xy（4y﹣2x﹣1）=﹣12xy2+6x2y+□，□的地方被钢笔水弄污了，你认为□内上应填写（ ）
A．3xy B．﹣3xy C．﹣1 D．1
二．填空题
8．（2015春•南长区期中）计算（﹣a4）（6a3﹣12a2+9a）= ，十边形的内角和是 ．2·1·c·n·j·y
9．（2014春•胶南市校级月考）= ．
10．（2013秋•万载县校级月考）若（x2+ax+1）•（﹣ax3）的展开式中，不含有x4项，则3a﹣1的值为 ．2-1-c-n-j-y
11．（2013春•富阳市校级期中）一个多项式与的积为x5y2﹣3x4y3﹣x3y4z，那么这个多项式为 ．【版权所有：21教育】
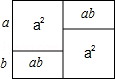
12．（2013秋•江油市校级月考）通过计算图中所示的几何图形的面积，可表示的代数恒等式是 ．21教育名师原创作品
13．（2011秋•淅川县期中）已知ab2=﹣3，则﹣ab（a2b5﹣ab3﹣b）= ．
三．解答题
14．（2014秋•陇西县期末）（1）计算：（）2÷（﹣）2
（2）计算：（x2y﹣xy2﹣y3）（﹣4xy2）．
15．若（am+b）•2a3b4=2a7b4+2a3bn（a≠0，a≠1，b≠0，b≠1）．求m+n的值．
16．若（1+x4ya）•（﹣xby）2=x16y4+x2b•y2，求ab的值．
17．（2015春•芦溪县期中）某同学在计算一个多项式乘以﹣2a时，因抄错运算符号，算成了加上﹣2a，得到的结果是a2+2a﹣1，那么正确的计算结果是多少？21世纪教育网版权所有
人教版八年级数学上册
14.1.4.2《单项式乘以多项式》同步训练习题（教师版）
一．选择题
1．（2015•黔东南州）下列运算正确的是（ ）
A．（a﹣b）2=a2﹣b2 B．3ab﹣ab=2ab C．a（a2﹣a）=a2 D．
选：B．
2．（2015春•岱岳区期末）如果长方体的长为3a﹣4，宽为2a，高为a，则它的体积是（ ）
A．3a2﹣4a B．a2 C．6a3﹣8a2 D．6a2﹣8a
考点： 单项式乘多项式；单项式乘单项式．21世纪教育网
分析： 直接利用单项式乘以多项式运算法则以及长方体体积公式得出即可．
解答： 解：由题意可得：
它的体积是：（3a﹣4）×2a×a=6a3﹣8a2．
故选：C．
点评： 此题主要考查了单项式乘以多项式，正确把握运算法则是解题关键．
3．（2015秋•重庆校级月考）化简x（2x﹣1）﹣x2（2﹣x）的结果是（ ）
A．﹣x3﹣x B．x3﹣x C．﹣x2﹣1 D．x3﹣1
考点： 单项式乘多项式．21世纪教育网
专题： 计算题．
分析： 原式利用单项式乘多项式法则计算，去括号合并即可得到结果．
解答： 解：原式=2x2﹣x﹣2x2+x3=x3﹣x，
故选B．
点评： 此题考查了单项式乘多项式，熟练掌握运算法则是解本题的关键．
4．（2015秋•遂宁校级月考）若三角形的底边为2m+1，高为2m，则此三角形的面积为（ ）
A．4m2+2m B．4m2+1 C．2m2+m D．2m2+m
考点： 单项式乘多项式．21世纪教育网
分析： 直接利用三角形面积公式结合单项式乘以多项式运算法则求出即可．
解答： 解：∵三角形的底边为2m+1，高为2m，
∴此三角形的面积为：×2m×（2m+1）=2m2+m．
故选：C．
点评： 此题主要考查了单项式乘以多项式以及三角形面积求法，正确掌握三角形面积求法是解题关键．
5．（2014春•南海区校级期中）下列计算正确的是（ ）
A．（﹣2a）•（3ab﹣2a2b）=﹣6a2b﹣4a3b
B．（2ab2）•（﹣a2+2b2﹣1）=﹣4a3b4
C．（abc）•（3a2b﹣2ab2）=3a3b2﹣2a2b3
D．（ab）2•（3ab2﹣c）=3a3b4﹣a2b2c
考点： 单项式乘多项式．21世纪教育网
分析： 根据单项式乘以多项式法则，对各选项计算后利用排除法求解．
解答： 解：A、应为（﹣2a）•（3ab﹣2a2b）=﹣6a2b+4a3b，故本选项错误；
B、应为（2ab2）•（﹣a2+2b2﹣1）=﹣2a3b2+4ab4﹣2ab2，故本选项错误；
C、应为（abc）•（3a2b﹣2ab2）=3a3b2c﹣2a2b3c，故本选项错误；
D、（ab）2•（3ab2﹣c）=3a3b4﹣a2b2c，正确．
故选D．
点评： 本题考查了单项式乘以多项式法则．单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加．要熟记单项式与多项式的每一项都相乘，不能漏乘．21教育网
6．（2013秋•鲤城区校级期末）三个连续的奇数，若中间一个为a，则它们的积为（ ）
A．a3﹣4a B．a3﹣6a C．4a3﹣a D．4a3﹣6a
考点： 单项式乘多项式．21世纪教育网
分析： 三个连续的奇数，若中间一个为a，则另外两个是a﹣2，a+2，求积即可．
解答： 解：三个连续的奇数，若中间一个为a，则另外两个是a﹣2，a+2．
则a（a﹣2）（a+2）=a3﹣4a．
故选A．
点评： 本题考查了整式的乘法，理解三个连续奇数的关系是关键．
7．（2013秋•合浦县期末）今天数学课上，老师讲了单项式乘以多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：﹣3xy（4y﹣2x﹣1）=﹣12xy2+6x2y+□，□的地方被钢笔水弄污了，你认为□内上应填写（ ）
A．3xy B．﹣3xy C．﹣1 D．1
考点： 单项式乘多项式．21世纪教育网
分析： 先把等式左边的式子根据单项式与多项式相乘，先用单项式乘多项式的每一项，再把所得的积相加，所得结果与等式右边的式子相对照即可得出结论．21·cn·jy·com
解答： 解：∵左边=﹣3xy（4y﹣2x﹣1）
=﹣12xy2+6x2y+3xy．
右边=﹣12xy2+6x2y+□，
∴□内上应填写3xy．
故选A．
点评： 本题考查的是单项式乘多项式，熟知单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加是解答此题的关键．
二．填空题
8．（2015春•南长区期中）计算（﹣a4）（6a3﹣12a2+9a）= ﹣4a7+8a6﹣6a5 ，十边形的内角和是 1440° ．21cnjy.com
9．（2014春•胶南市校级月考）= ﹣a2b3+a2b2﹣ab2 ．
考点： 单项式乘多项式．21世纪教育网
分析： 根据单项式与多项式相乘，先用单项式乘多项式的每一项，再把所得的积相加计算即可．
解答：
解：=﹣a2b3+a2b2﹣ab2．
故答案为：﹣a2b3+a2b2﹣ab2．
点评： 本题考查了单项式与多项式相乘，熟练掌握运算法则是解题的关键，计算时要注意符号的处理．
10．（2013秋•万载县校级月考）若（x2+ax+1）•（﹣ax3）的展开式中，不含有x4项，则3a﹣1的值为 0 ．www.21-cn-jy.com
考点： 单项式乘多项式．21世纪教育网
分析： 单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加．先依据法则运算，展开式后，因为不含x4项，所以x4项的系数为0，再求a的值．www-2-1-cnjy-com
解答： 解：（x2+ax+1）（﹣ax3）=﹣ax5﹣a2x4﹣ax3，
展开式中不含x4项，则a2=0，
∴a=0．
∴3a﹣1=1﹣1=0，
故答案是：0．
点评： 本题考查了单项式与多项式相乘，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．
11．（2013春•富阳市校级期中）一个多项式与的积为x5y2﹣3x4y3﹣x3y4z，那么这个多项式为 ﹣2x2+6xy+2y2z ．21·世纪*教育网
考点： 单项式乘多项式．21世纪教育网
专题： 计算题．
分析： 根据题意列出关系式，利用多项式除单项式法则计算即可得到结果．
解答：
解：根据题意得：（x5y2﹣3x4y3﹣x3y4z）÷（﹣x3y2）=﹣2x2+6xy+2y2z．
故答案为：﹣2x2+6xy+2y2z
点评： 此题考查了单项式乘多项式，根据题意列出正确的算式是解本题的关键．
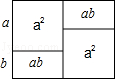
12．（2013秋•江油市校级月考）通过计算图中所示的几何图形的面积，可表示的代数恒等式是 2a（a+b）=2a2+2ab ． 21*cnjy*com
考点： 单项式乘多项式．21世纪教育网
分析： 本题所给的图中，四个小图形的面积与大图形的面积相等，据此列出代数式即可解答．
解答： 解：由题意可知2a（a+b）=2a2+2ab．
故答案为：2a（a+b）=2a2+2ab．
点评： 本题考查了单项式与多项式相乘，用不同方法表示面积是解题的关键．
13．（2011秋•淅川县期中）已知ab2=﹣3，则﹣ab（a2b5﹣ab3﹣b）= 33 ．
考点： 单项式乘多项式；代数式求值．21世纪教育网
专题： 整体思想．
分析： 对所给的式子变形提取公因式b，使其中出现ab2的因式，然后利用整体代入法计算．
解答： 解：﹣ab（a2b5﹣ab3﹣b），
=﹣ab2（a2b4﹣ab2﹣1），
当ab2=﹣3时，
原式=﹣（﹣3）[（﹣3）2﹣（﹣3）﹣1]=33；
故填：33．
点评： 本题考查了提公因式法分解因式，提取公因式b出现已知条件的形式比较关键，灵活运用此法则，可简便运算．【来源：21cnj*y.co*m】
三．解答题
14．（2014秋•陇西县期末）（1）计算：（）2÷（﹣）2
（2）计算：（x2y﹣xy2﹣y3）（﹣4xy2）．
考点： 单项式乘多项式；分式的乘除法．21世纪教育网
分析： （1）先算乘方，再把除法转化成乘法，最后约分即可；
（2）根据单项式与多项式相乘，先用单项式乘多项式的每一项，再把所得的积相加计算即可．
解答：
解：（1）（）2÷（﹣）2=×=；
（2）（x2y﹣xy2﹣y3）（﹣4xy2）=﹣3x3y3+2x2y4+xy5；
点评： 此题考查了单项式乘多项式和分式的乘除法，熟练掌握运算法则是解题的关键，计算时要注意符号的处理．【出处：21教育名师】
15．若（am+b）•2a3b4=2a7b4+2a3bn（a≠0，a≠1，b≠0，b≠1）．求m+n的值．
考点： 单项式乘多项式．21世纪教育网
分析： 利用单项式与多项式相乘的运算法则求解即可．
解答： 解：∵（am+b）•2a3b4=2a7b4+2a3bn，
∴2a3+mb4+2a3b5=2a7b4+2a3bn，
∴3+m=7，n=5，解得m=4，n=5，
∴m+n=4+5=9．
点评： 本题主要考查了单项式与多项式相乘的运算法则，解题的关键是熟记单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加．
16．若（1+x4ya）•（﹣xby）2=x16y4+x2b•y2，求ab的值．
考点： 单项式乘多项式．21世纪教育网
分析： 先利用单项式与多项式相乘的运算法则计算，再利用对应的项求解即可．
解答： 解：∵（1+x4ya）•（﹣xby）2=x16y4+x2b•y2，
∴x2by2+x4+2bya+2=x16y4+x2b•y2，
∴x4+2bya+2=x16y4，可得4+2b=16，a+2=4，解得b=6，a=2，
∴ab=2×6=12．
点评： 本题主要考查了单项式乘多项式，解题的关键是找准对应项．
17．（2015春•芦溪县期中）某同学在计算一个多项式乘以﹣2a时，因抄错运算符号，算成了加上﹣2a，得到的结果是a2+2a﹣1，那么正确的计算结果是多少？【来源：21·世纪·教育·网】
．