二次函数与一元二次方程

1．对抛物线y＝－x²＋2x－3而言，下列结论正确的是(　D　)

A．与x轴有两个交点

B．开口向上

C．与y轴的交点坐标是(0，3)

D．顶点坐标是(1，－2)

【解析】 A项，∵Δ＝2²－4×(－1)×(－3)＝－8＜0，∴抛物线与x轴无交点，本选项错误；B项，∵二次项系数－1＜0，∴抛物线开口向下，本选项错误；C项，当x＝0时，y＝－3，∴抛物线与y轴交点坐标为(0， －3)，本选项错误；D项，∵y＝－x²＋2x－3＝－(x－1)²－2，∴抛物线顶点坐标为(1，－2)，本选项正确．故选D.

2．抛物线y＝－3x²－x＋4与坐标轴的交点的个数是(　A　)

A．3　　　　B．2　　　C．1　　　D．0

【解析】 抛物线解析式y＝－3x²－x＋4中，令x＝0，得y＝4，∴抛物线与y轴的交点为(0，4)；令y＝0，得到－3x²－x＋4＝0，即3x²＋x－4＝0，解得x₁＝－，x₂＝1，∴抛物线与x轴的交 点分别为，(1，0)．综上，抛物线与坐标轴的交点个数为3.

3．[2012·资阳]如图22－2－1是二次函数y＝ax²＋bx＋c的部分图象，由图象可知不等式ax²＋bx＋c＜0的解集是(　D　)

A．－1＜x＜5

B．x＞5

C．x＜－1且x＞5

D．x＜－1或x＞5

【解析】 由图象得：抛物线的对称轴是x＝2，抛物线与x轴的一个交点的坐标为(5，0)，∴抛物线与x轴的另一个交点的坐标为(－1，0)．利用图象可知：ax²＋bx＋c＜0的解集即是y＜0的解集，即x＜－1或x＞5.

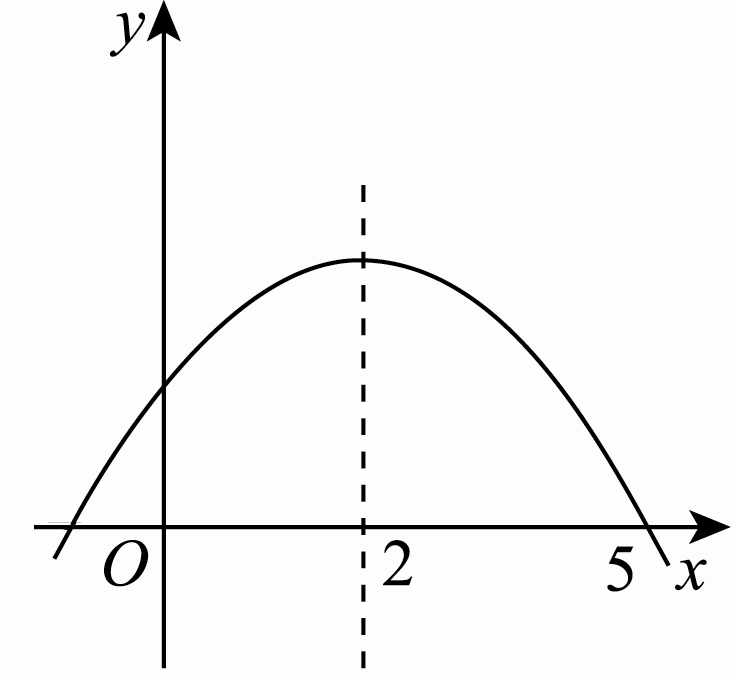
图22－2－1

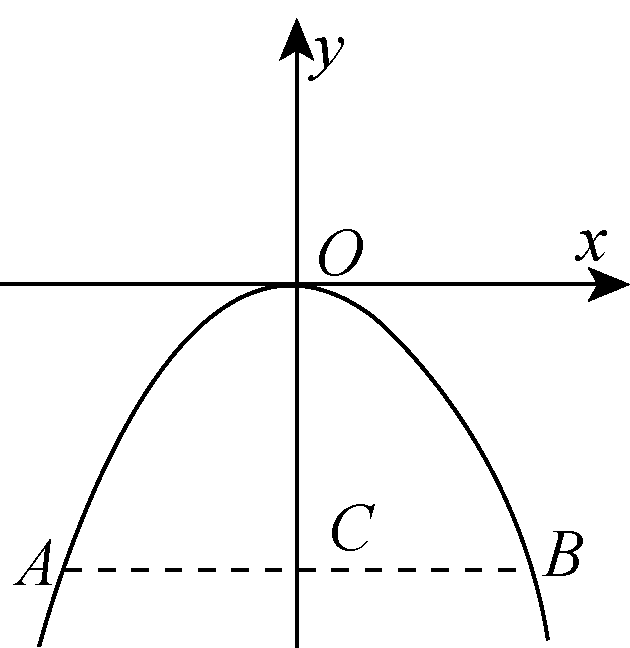
图22－2－2

4．某涵洞的形状是抛物线形，解析式为y＝－x²，它的截面如图22－2－2所示，现测得涵洞的顶点O到水面的距离为9 m，则水面宽AB为(　B　)

A．3 m B．6 m

C．9 m D．18 m

【解析】 设B点的横坐标为x₀，根据题意得－x₀²＝－9，x₀²＝9，x₀＝3，所以AB＝2x₀＝6.

5．[2013·济宁]二次函数y＝ax²＋bx＋c(a≠0)的图象如图22－2－3所示，则下列结论中正确的是(　B　)

图22－2－3

A．a>0

B．当－1<x<3时，y>0

C．c<0

D．当x≥1时，y随x的增大而增大

6．已知抛物线与x轴的一个交点为A(1，0)，对称轴是x＝－1，则抛物线与x轴的另一交点的坐标是(　B　)

A．(－2，0) B．(－3，0)

C．(－4，0) D．(－5，0)

【解析】 设抛物线与x轴的另一个交点为B(b，0)，∵抛物线与x轴的一个交点为A(1，0)，对称轴是x＝－1，∴＝－1，解得b＝－3，∴B(－3，0)．

7．若二次函数y＝－x²＋2x＋k的部分图象如图22－2－4所示，关于x的一元二次方程－x²＋2x＋k＝0的一个解x₁＝3，则另一个解x₂＝__－1__．

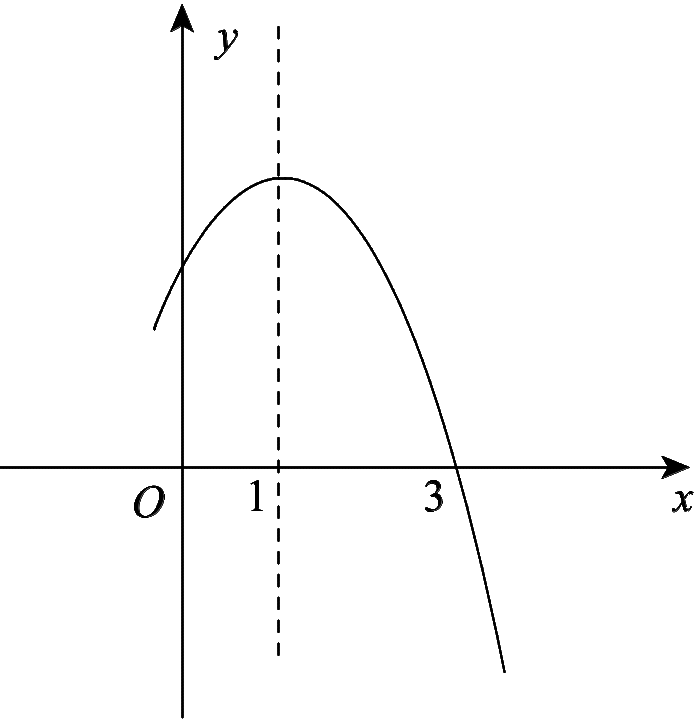
图22－2－4

【解析】 根据二次函数图象的对称性知图象与x轴的另一个交点为(－1，0)，则另一个解x₂＝－1.

8．如图22－2－5，已知二次函数 y＝－x²＋x＋4的图象与y轴交于点A，与x轴交于B，C两点，则点A的坐标为__(0，4)__，点C的坐标为__(8，0)__．

【解析】 令y＝0，则－x²＋x＋4＝0，解得x₁＝－2，x₂＝8，所以点C的坐标为(8，0)；令x＝0，得y＝4，所以点A的坐标为(0，4)．

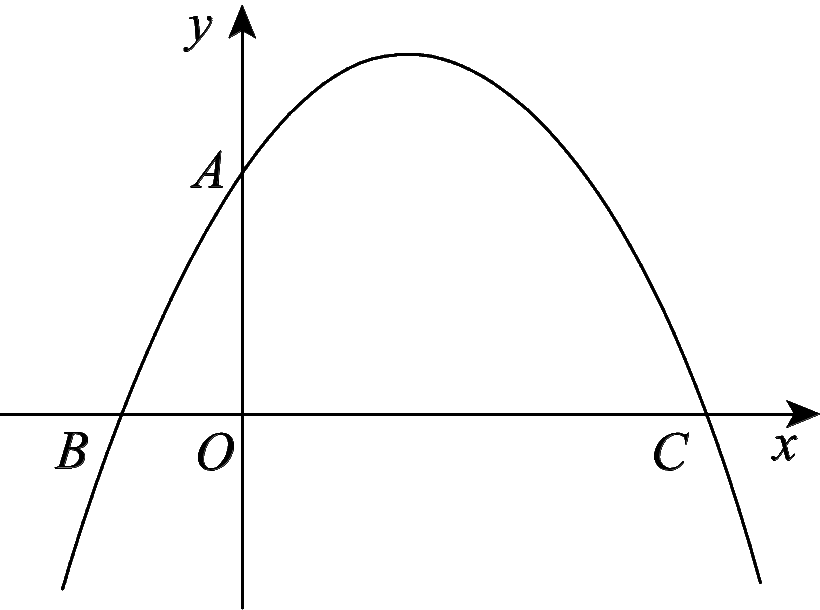
图22－2－5

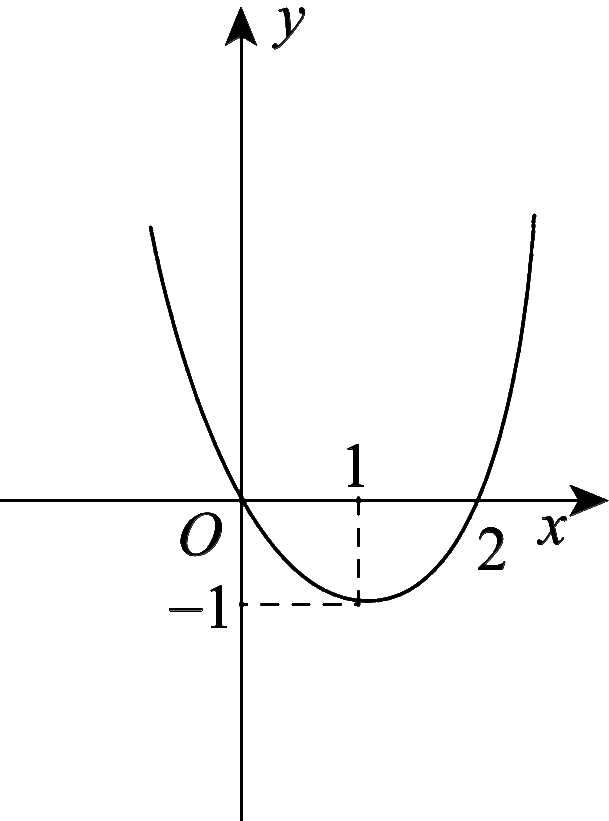
图22－2－6

9．已知二次函数y＝ax²＋bx＋c的图象如图22－2－6所示，则

(1)这个二次函数的解析式为__y＝x²－2x__；

(2)当x＝__－1或3__时，y＝3；

(3)根据图象回答：

当__x＜0或x＞2__时，y＞0；

当0＜x＜2时，y＜0.

【解析】 设二次函数解析式为y＝a(x－1)²－1，

∵图象过(0，0)点，∴0＝a(0－1)²－1，

∴a＝1，∴ y＝(x－1)²－1，即y＝x²－2x.

令y＝3，得x²－2x＝3，x²－2 x－3＝0，解得x₁＝－1，x₂＝3，所以当x＝－1或3时，y＝3.

观察图象可得y＞0和y＜0时对应的x的取值范围．

10．如图22－2－7，在平面直角坐标 系中，抛物线y＝ax²＋bx＋c(a≠0)的图象经过M(1，0)和N(3，0)两点，且与y轴交于点D(0，3)，求该抛物线的解析式．

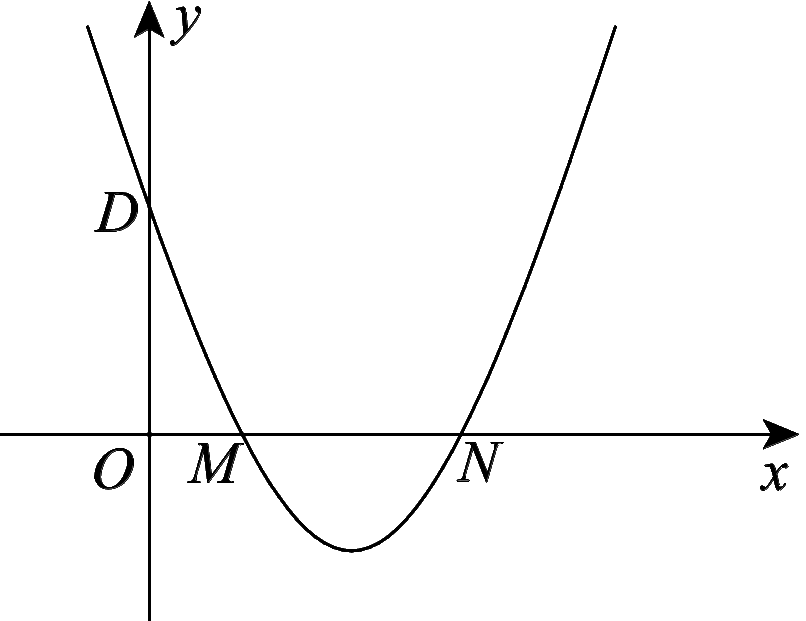
图22－2－7

解：∵抛物线y＝ax²＋bx＋c(a≠0)的图象经过M(1，0)和N(3，0)两点，∴可设抛物线的解析式为y＝a(x－1)(x－3)．

∵抛物线与y轴交于点D(0，3)，

∴把D点坐标代入y＝a(x－1)(x－3)得a＝1，

∴y＝x²－4x＋3.

11．已知二次函数 y＝x²－3x＋m(m为常数)的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程x²－3x＋m＝0的两实数根是(　B　)

A．x₁＝1，x₂＝－1 B．x₁＝1，x₂＝2

C．x₁＝1，x₂＝0 D．x₁＝1，x₂＝3

【解析】 ∵二次函数的解析式是y＝x²－3x＋m(m为常数)，

∴该抛物线的对称轴是x＝.

又∵二次函数y＝x²－3x＋m(m为常数)的图象与x轴的一个交点为(1，0)，

∴根据抛物线的对称性质知，该抛物线与x轴的另一个交点是(2，0)，

∴关于x的一元二次方程x²－3x＋m＝0的两实数根分别是x₁＝1，x₂＝2.

12．二次函数y＝ax²＋bx＋c的图象如图22－2－8所示，则下列关系式错误的是(　D　)

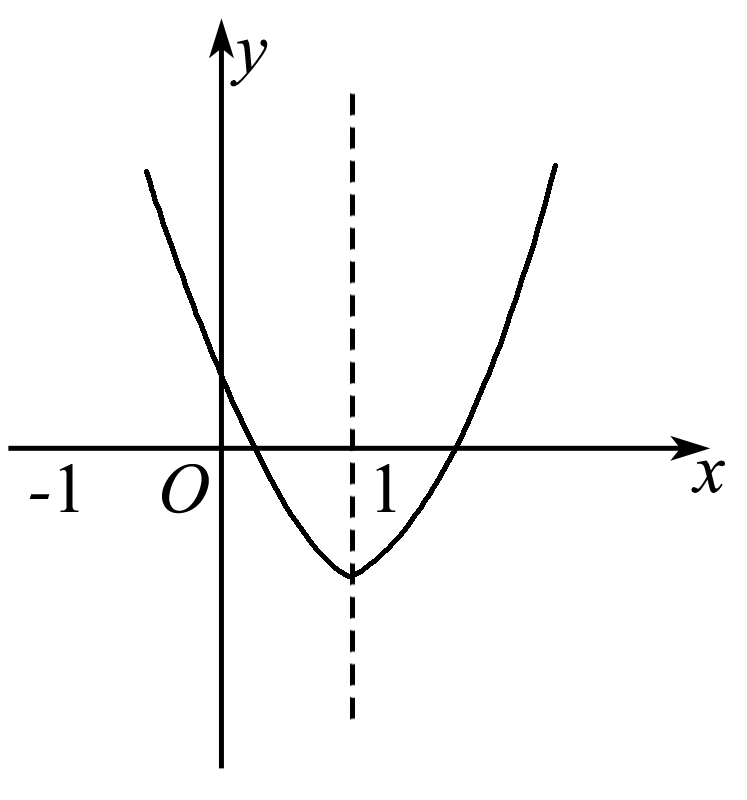
图22－2－8

A．a＞0 B．c＞0

C．b²－4a c＞0 D．a＋b＋c＞0

【解析】 A．∵抛物线的开口向上，

∴a＞0，正确；

B．∵抛物线与y轴的交点在y轴的正半轴上，

∴c＞0，正确；

C．∵抛物线与x轴有两个交点，

∴b²－4ac＞0，正确；

D．把x＝1代入抛物线的解析式 得：y＝a＋b＋c＜0，错误，故选D.

13．已知二次函数y＝ax²＋bx＋c的图象如图22－2－9所示，对称轴是直线x＝1.下列结论：①abc＞0，②2a＋b＝0，③b²－4ac＜0，④4a＋2b＋c＞0

其中正确的是(　C　)

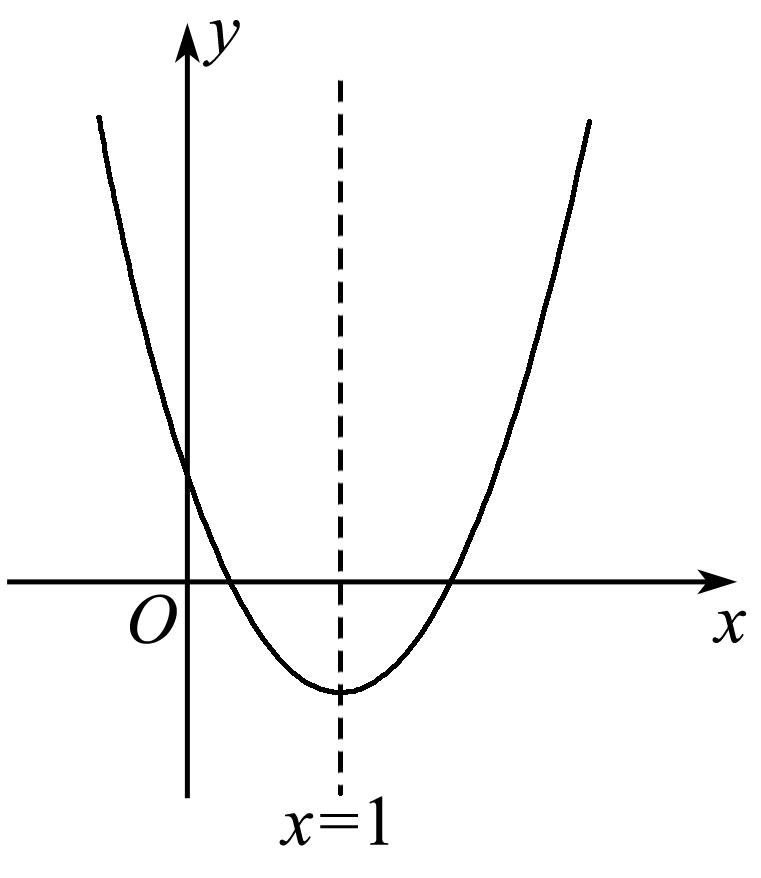
图22－2－9

A．①③ B．只有②

C．②④ D．③④

【解析】　∵抛物线的开口向上，

∴a＞0，

∵－＞0，∴b＜0，

∵抛物线与y轴交于正半轴，

∴c＞0，

∴abc＜0，①错误；

∵对称轴为直线x＝1，

∴－＝1，即2a＋b＝0，②正确，

∵抛物线与x轴有2个交点，

∴b²－4ac＞0，③错误；

∵对称轴为直线x＝1，

∴x＝2与x＝0时的函数值相等，而x＝0时对应的函数值为正数，

∴4a＋2b＋c＞0，④正确；

则其中正确的有②④ .

14. 若函数y＝mx²＋2x＋1的图象与x轴只有一个公共点，则常数m的值是__0或1__．

【解析】 (1)若m＝0，则函数y＝2x＋1，是一次函数，与x轴只有一个交点；

(2)若m≠0，则函数y＝mx²＋2x＋1，是二次函数．

根据题意得Δ＝4－4m＝0，

解得m＝1.

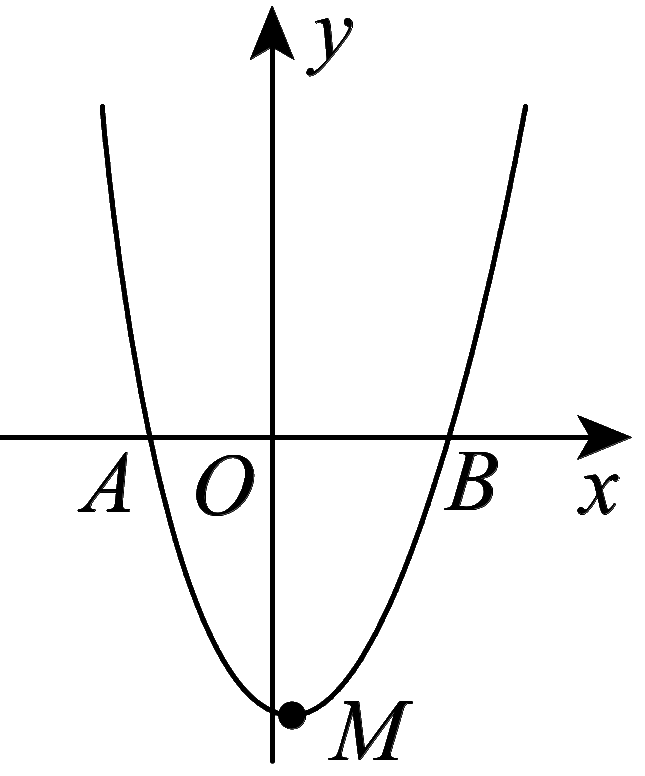
图22－2－10

15．如图22－2－10，二次函数y＝x²－x＋c的图象与x轴分别交于A，B两点，顶点M关于x轴的对称点是M′.

(1)若A(－4，0)，求二次函数的解析式；

(2)在(1)的条件下，求四边形AMBM′的面积．

解：(1)∵点A(－4，0)在二次函数y＝x²－x＋c的图象上，∴0＝×(－4)²－(－4)＋c，

解得c＝－12，

∴二次函数 的关系式为y＝x²－x－12.

(2)由(1)知y＝x²－x－12，

∴－＝－＝1.

当x＝1时，y＝×1²－1－12＝－，

∴M.

令y＝0，得x²－x－12＝0，解得x₁＝－4，x2＝6，

∴B(6，0)，AB＝＝10.

又∵点M′与点M关于x轴对称，

∴S_{四边形AMBM ′}＝×AB××2＝125.

16．已知：一元二次方程x²＋kx＋k－＝0

(1)求证：不论k为何实数，此方程总有两个实数根；

(2)设k<0，当二次函数y＝x²＋kx＋k－的图象与x轴的两个交点A，B间的距离为4时，求出此二次函数的解析式．

解：(1)证明：∵Δ＝k²－4·(k－)＝k²－2k＋1＝(k－1)²

不论k为何实数，(k－1)²≥0

∴不论k为何实数，此方程总有两个实数根；

(2)∵二次函数y＝x²＋kx＋k－的图象与x轴的两个交点A，B间的距离为4.

∴2＝4，

∴(k－1)²＝4

解得k₁＝3，k₂＝－1

又∵k<0

∴k＝ －1.

∴y＝x²－x－

17．已知二次函数y＝k(x＋1)与x轴交于点A，B，与y轴交于点C，则能使△ABC为等腰三角形的抛物线的条数是(　C　)

A．2 B．3 C．4 D．5

【解析】 y＝k(x＋1)＝(x＋1)(kx－3)，所以抛物线经过点A(－1，0)，B，C(0，－3)，所以AC＝＝＝.①当k>0，点B在x轴的正半轴时，若AC＝BC，则＝，解得k＝3；若AC＝AB，则＋1＝，解得k＝；若AB＝BC，则＋1＝，解得k＝.②当k<0，点B在x轴的负半轴时，点B只能在点A的左侧，只可能有AC＝AB，则－1－＝，解得k＝－，所以能使△ABC为等腰三角形的抛 物线共有4条，故选C.