河北省衡水中学2016届高三上学期第七次调研考试
文数试题
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一![]() 项
项
是符合题目要求的.
1.已知集合![]() ,则
,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() 是虚数单位,复数
是虚数单位,复数![]() (
)[来源:Zxxk.Com]
(
)[来源:Zxxk.Com]
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知双曲线![]() 的离心率为
的离心率为![]() ,则
,则![]() 的渐近线方程为(
)
的渐近线方程为(
)
A.
![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.![]() 已知向量
已知向量![]() ,向量
,向量![]() ,则
,则![]() (
)
(
)
A.-1 B.0 C.1 D.2
5.设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() (
)
(
)
A.5 B. 7 C.9 D.11
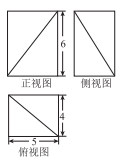
6.一个长方体被一个平面截去一部分后所剩几何体的三视图如图所示(单位:![]() ),则该几何体的体积为(
)
),则该几何体的体积为(
)
A.120![]() B.80
B.80![]() C.100
C.100![]() D.60
D.60![]()
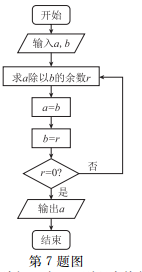
7.某算法的程序框图如图所示,若![]() 输入的
输入的![]() 的值分别为60与32,则程序执行后的结果是(
)
的值分别为60与32,则程序执行后的结果是(
)
A.0 B. 4 C.7 D.28[来源:学。科。网]
8.已知等比数列![]() 满足
满足![]() ,则
,则![]() (
)
(
)
A.2
B.
1 C.
![]() D.
D.![]()
9.设实数![]() 满足
满足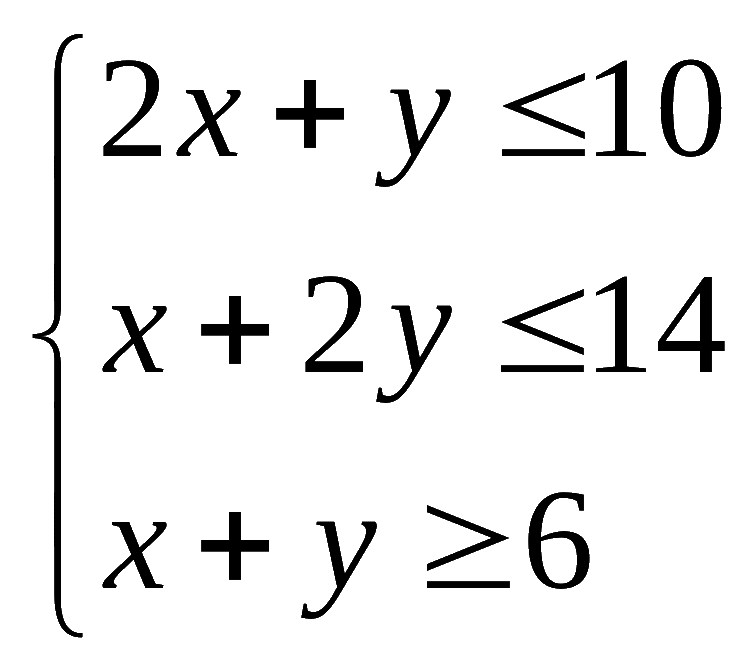 ,则
,则![]() 的最
的最![]() 大值为(
)
大值为(
)
A.![]() B.
B.
![]() C.
12
C.
12
![]() D.14
D.14
10.点![]() 在同一个球的球面上,
在同一个球的球面上,![]() ,若四面体
,若四面体![]() 体积的最大值为
体积的最大值为![]() ,则这个球的表面积为(
)
,则这个球的表面积为(
)
A.![]() B.
B.
![]() C.
C.![]() D.
D.![]()
11.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲,乙,丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )
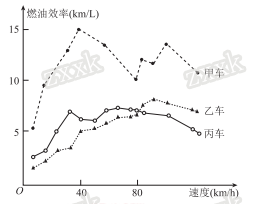
消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小![]() 时的速度行驶1小时,消耗10升汽油
时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油
12.已知函数![]() 满足
满足![]() ,且
,且![]() 分别是
分别是![]() 上的偶函数和奇函数,若
上的偶函数和奇函数,若![]() 使得不等式
使得不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是(
)
的取值范围是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(共90分)[来源:Z§xx§k.Com]
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.给出下列命题:
①![]() 线性相关系数
线性相关系数![]() 越大,两个变量的线性相关越强;反之,线性相关性越弱;
越大,两个变量的线性相关越强;反之,线性相关性越弱;
②由变量![]() 和
和![]() 的数据得到其回归直线方程:
的数据得到其回归直线方程:![]() ,则
,则![]() 一定经过
一定经过![]() ;
;
③从越苏传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
④在回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
⑤在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 增加0.1个单位,其中真命题的序号是
.
增加0.1个单位,其中真命题的序号是
.
14.在三棱锥![]() 内任取一点
内任取一点![]() ,使得
,使得![]() 的概率是
.
的概率是
.
15.已知圆![]() 和两点
和两点![]() ,若圆上存在点
,若圆上存在点![]() ,使得
,使得![]() ,则
,则![]() 的取值范围是
.
的取值范围是
.
16.已知曲线![]() 在
在![]() 点
点![]() 处
处![]() 的切线与曲线
的切线与曲线![]() 相切,则
相切,则![]()
![]() .
.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的值;
的值;
(2)若![]() 边上中线
边上中线![]() ,求
,求![]() 的面积.
的面积.
18(本小题满分12分)某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:

(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(2)质检部门从该车间甲,![]() 乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”
乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”![]() ,求该车间“质量合格”的概率.
,求该车间“质量合格”的概率.
19.(本小题满分12分)已知在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,若
是平行四边形,若![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
20.(本小题满分12分)已知![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() ,线段
,线段![]() 的垂直平分线与半径
的垂直平分线与半径![]() 相交于点
相交于点![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() 的方程;
的方程;
(1)求曲线![]() 的方程;
的方程;
(2)当点![]() 在第一象限,且
在第一象限,且![]() 时,求点
时,求点![]() 的坐标.
的坐标.
21.(本小题满分12分)已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值
上的最大值和最小值![]() ;
;
(3)求证:![]() .
.
请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
22.(本小题满分1![]() 0分)选修4-1:几何证明选讲
0分)选修4-1:几何证明选讲
如图,直线![]() 为圆的切线,切点为
为圆的切线,切点为![]() ,点
,点![]() 在圆上,
在圆上,![]() 的角平分线
的角平分线![]() 交圆于点
交圆于点![]() 垂直
垂直![]() 交圆于点
交圆于点![]() .
.![]() [来源:学+科+网]
[来源:学+科+网]
(1)证明:![]()
(2)设圆的半径为1,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,求
,求![]() 外接圆的半径.
外接圆的半径.

23.(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为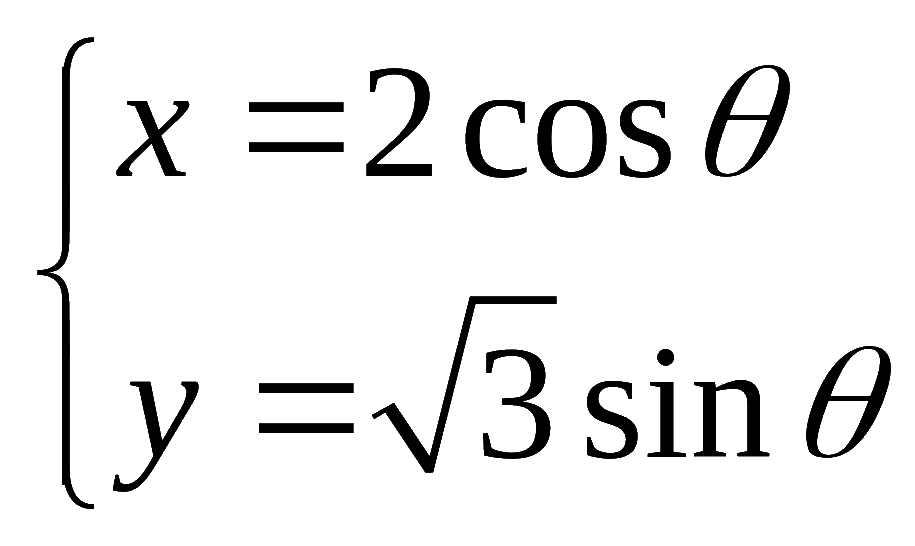 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)分别写出![]() 的普通方程,
的普通方程,![]() 的直角坐标方程;
的直角坐标方程;
(2)已知![]() 分别为曲线
分别为曲线![]() 的上,下顶点,点
的上,下顶点,点![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的最大值
的最大值
24.(本小题满分10分)选修4-5:不等式选讲[来源:Zxxk.Com]
已知函数![]() 的定义域为
的定义域为![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]()
![]() 的最大值为
的最大值为![]() ,当正数
,当正数![]() 满足
满足![]() 时,求
时,求![]() 的最小值.
的最小值.