19.2 一次函数
第6课时 一次函数与一元一次方程、不等式
基础训练
知识点1一次函数与一元一次方程
1.方程x+1=0的解就是函数y=x+1的图象与( )
A.x轴交点的横坐标 B.y轴交点的横坐标
C.y轴交点的纵坐标 D.x轴交点的纵坐标
2.下列说法中,正确的是( )
A.方程2x-6=0的解可以看成直线y=2x-6与y轴交点的横坐标
B.方程2x-6=0的解可以看成直线y=2x-6与x轴交点的横坐标
C.方程2x=6的解可以看成直线y=2x+6与y轴交点的横坐标
D.方程2x=6的解可以看成直线y=2x+6与x轴交点的横坐标
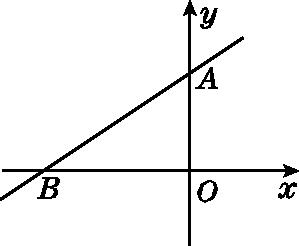
3.(2016·桂林)如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )21世纪教育网版权所有

A.x=2 B.x=0
C.x=-1 D.x=-3
4.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是( )
A.x=2 B.x=4 C.x=8 D.x=10
5.一元一次方程ax-b=0的解是x=3,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-3,0) B.(3,0) C.(a,0) D.(-b,0)
6.已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解可能是( )
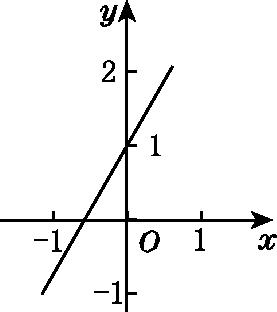
A.x=1 B.x=Error: Reference source not found
C.x=-Error: Reference source not found D.x=-1
知识点2一次函数与一元一次不等式
7.已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),
则当x 时,y≤0.
8.(2016·百色)直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A.x≤3 B.x≥3 C.x≥-3 D.x≤0
9.如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式Error: Reference source not foundx>kx+b>-2的解集为( )www.21-cn-jy.com

A.x<2 B.x>-1
C.x<1或x>2 D.-1<x<2
10.若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
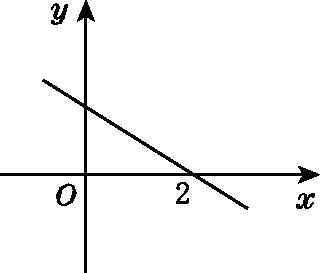
A.x<2 B.x>2 C.x<5 D.x>5
11.一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )21cnjy.com

![]()
易错点 利用函数图象解不等式时,对函数值和点的坐标的关系不理解导致出错(数形结合思想)
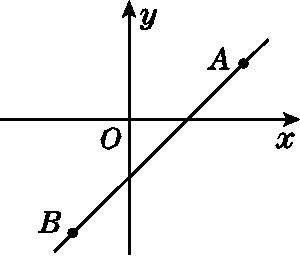
12.如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的解集为 . 2·1·c·n·j·y
提升训练
考查角度1利用一个一次函数图象解一元一次方程、不等式
13.画出函数y=2x+6的图象,利用图象:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>0的解集;
(3)若-2≤y≤2,请直接写出x的取值范围.

考查角度2利用两个一次函数图象解一元一次方程、不等式
14.如图,对照图象,请回答下列问题:
(1)当x取何值时,2x-5=-x+1?
(2)当x取何值时,2x-5>-x+1?
(3)当x取何值时,2x-5<-x+1?

探究培优
拔尖角度1利用一次函数解一元一次方程综合应用问题
15.已知某市的光明中学、市图书馆和光明电影院在同一直线上,它们之间的距离如图所示.小张星期天上午带了75元现金先从光明中学乘出租车去了市图书馆,付费9元,中午再从市图书馆乘出租车去了光明电影院,付费12.6元.若该市出租车的收费标准是:不超过3公里计费为m元,3公里后按n元/公里计费.21教育网
(1)求m,n的值,并直接写出车费y(元)与路程x(公里)(x>3)之间的函数关系式.
(2)如果小张这天外出的消费还包括:中午吃饭花费15元,在光明电影院看电影花费25元.问小张剩下的现金够不够乘出租车从光明电影院返回光明中学?为什么?21·cn·jy·com
![]()
拔尖角度2利用一次函数解与不等式综合应用问题
16.(2016·临沂)现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.【来源:21·世纪·教育·网】
(1)请分别写出甲、乙两家快递公司快递物品的费用y(元)与x(千克)之间的函数解析式;
(2)小明选择哪家快递公司更省钱?
参考答案
1.【答案】A 2.【答案】B
3.【答案】D
解:方程ax+b=0的解,即为函数y=ax+b的图象与x轴交点的横坐标.
∵直线y=ax+b过点B(-3,0),
∴方程ax+b=0的解是x=-3.
故选D.
4.【答案】A
5.【答案】B 6.【答案】C 7.【答案】≥2
8.【答案】A
解:首先把点A(2,1)的坐标代入y=kx+3中,可得k的值,再解不等式kx+3≥0即可.
9.【答案】D
解:把A(2,1),B(-1,-2)两点的坐标分别代入y=kx+b,得Error: Reference source not found解得Error: Reference source not found解不等式组Error: Reference source not foundx>x-1>-2,得-1<x<2.21·世纪*教育网
10.【答案】C
11.【答案】C
解:从图象得到,当x>-2时,y=3x+b的图象在函数y=ax-3的图象上面,所以不等式3x+b>ax-3的解集为x>-2.故选C.www-2-1-cnjy-com
12.【答案】-1<x<2
解:此题运用数形结合思想,观察图象知不等式-2<kx+b<1的解集就是线段AB(不包含端点)所对应的自变量x的取值范围.21*cnjy*com
13.解:图象如图:
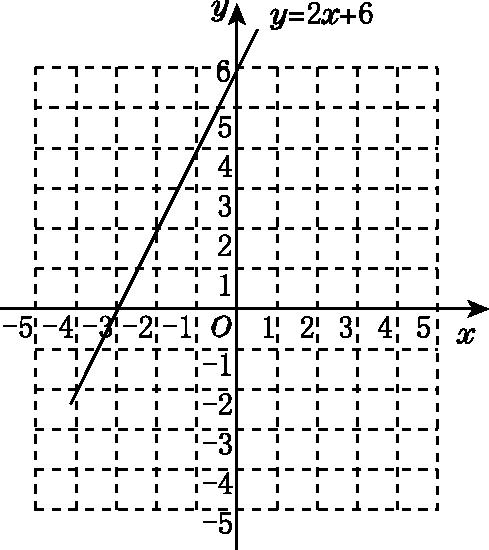
(1)观察图象知:该函数图象经过点(-3,0),
故方程2x+6=0的解为x=-3;
(2)观察图象知:当x>-3时,y>0,
故不等式2x+6>0的解集为x>-3;
(3)当-2≤y≤2时,x的取值范围为-4≤x≤-2.
14.解:(1)由图象可知,直线y=2x-5与直线y=-x+1的交点的横坐标是2,所以当x取2时,2x-5=-x+1.2-1-c-n-j-y
(2)由图象可知,当x>2时,直线y=2x-5落在直线y=-x+1的上方,即2x-5>-x+1.
(3)由图象可知,当x<2时,直线y=2x-5落在直线y=-x+1的下方,即2x-5<-x+1.
15.解:(1)由题图可知光明中学和市图书馆相距2公里,付费9元,
所以m=9.
因为从市图书馆乘出租车去光明电影院,路程为5公里,付费12.6元,
所以(5-3)n+9=12.6,
解得n=1.8.
所以车费y(元)与路程x(公里)(x>3)之间的函数关系式
为:y=1.8(x-3)+9=1.8x+3.6(x>3).
(2)不够.理由如下:小张剩下的现金为:75-15-25-9-12.6=13.4(元),
乘出租车从光明电影院返回光明中学的费用:1.8×(2+5)+3.6=16.2(元)
因为13.4<16.2,
故小张剩下的现金不够乘出租车从光明电影院返回光明中学.
16.解:(1)由题意知y甲=Error: Reference source not found
y乙=16x+3.
(2)①当0<x≤1时,
令y甲<y乙,即22x<16x+3,
解得0<x<Error: Reference source not found;
令y甲=y乙,即22x=16x+3,
解得x=Error: Reference source not found;
令y甲>y乙,即22x>16x+3,
解得Error: Reference source not found<x≤1.
②当x>1时,
令y甲<y乙,即15x+7<16x+3,
解得x>4;
令y甲=y乙,即15x+7=16x+3,
解得x=4;
令y甲>y乙,即15x+7>16x+3,
解得1<x<4.
答:当Error: Reference source not found<x<4时,选乙快递公司省钱;当x=4或x=Error: Reference source not found时,选甲、乙两家快递公司快递费一样多;当0<x<Error: Reference source not found或x>4时,选甲快递公司省钱.